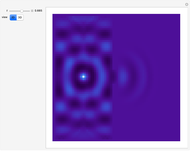
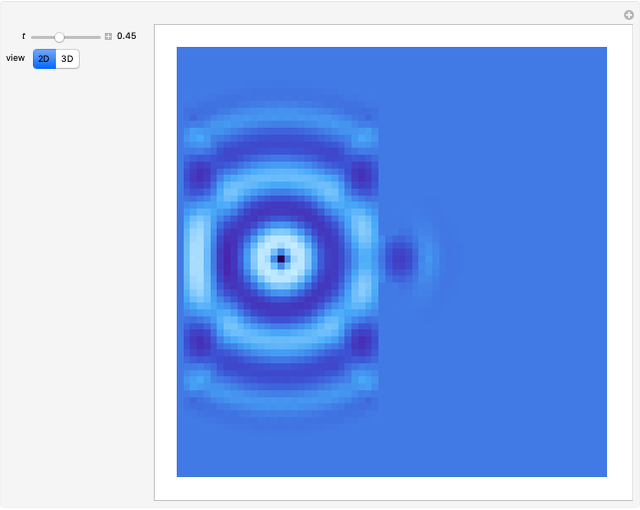
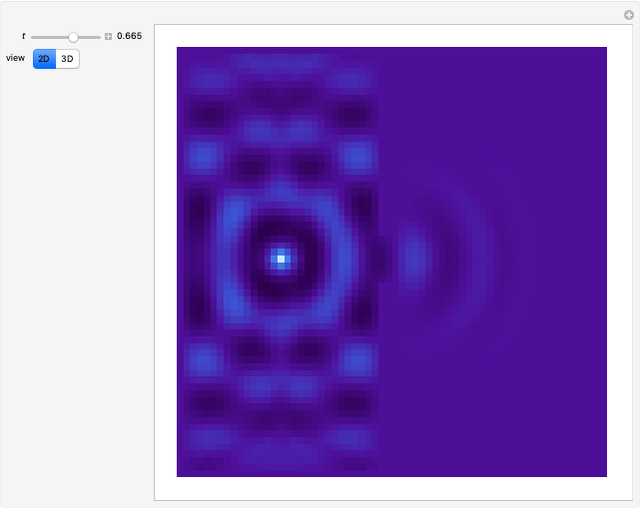
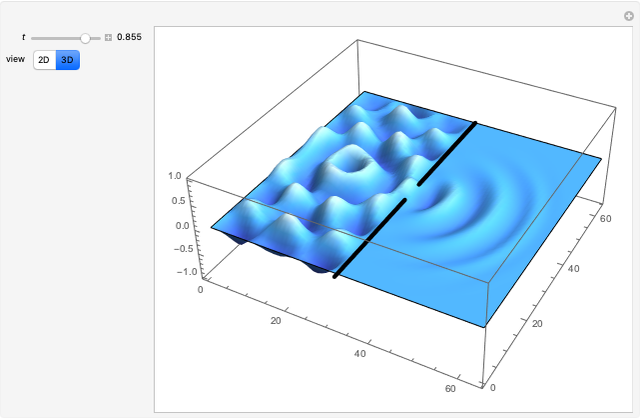
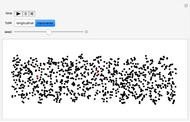
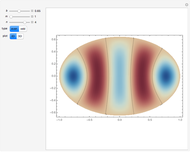
Water Ripples Passing through a Slit

The procedure is very simple, with surprising results, and is used to represent fluids in video games [1]. It is based on the fact that the wave equation (a second-order PDE) can be rewritten as a system of two first-order PDEs

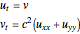
for which a possible discretization is

.

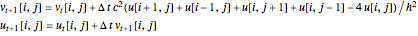An implementation with some variations can be found at [2], with an updating scheme is based on [3]: given two arrays, 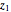for the time and 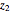representing 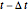. From an element in 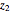, the sum of the four neighbors that appear in the discretization of a component in 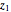is subtracted, giving an updated value for 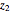, with the exception of positions at the walls. A CFL constant (Courant–Friedrichs–Lewy condition) is necessary to ensure stability.

References

[1] M. Müller. "Real Time Fluids in Games." (Nov 29, 2012) www.matthiasmueller.info/talks/gameFluids2007.pdf.

[2] P. Nylander. "Fluid Motion Simulations and Artwork." (Nov 29, 2012) www.bugman123.com/FluidMotion/index.html.

[3] H. Elias. "2D Water." (Nov 29, 2012) freespace.virgin.net/hugo.elias/graphics/x_water.htm.