Zero-Pole Cancellation in Transfer Functions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
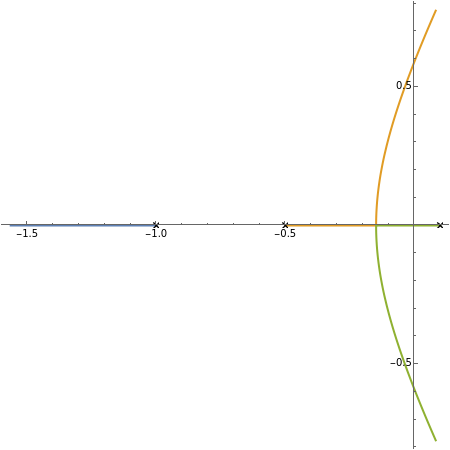
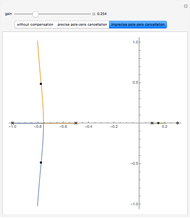
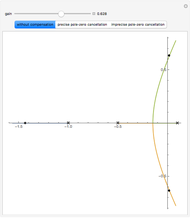
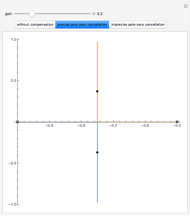
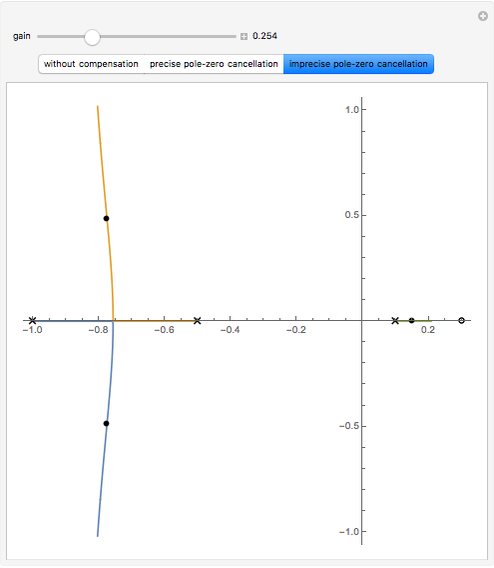
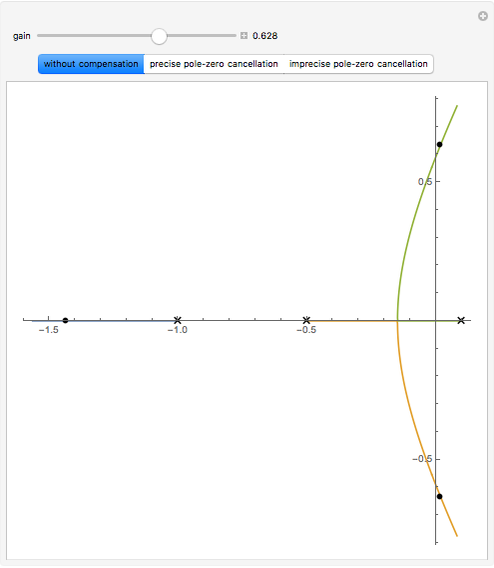
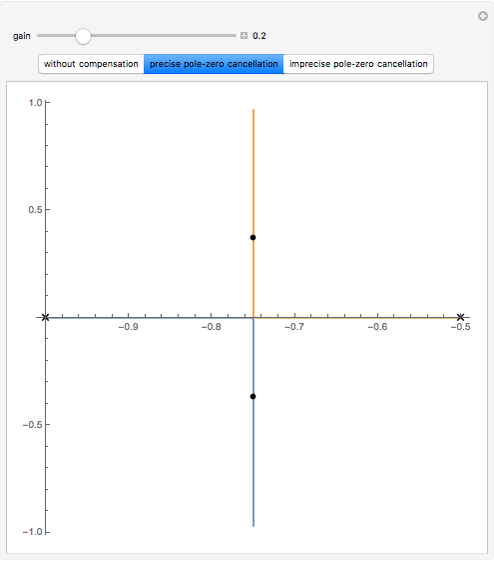
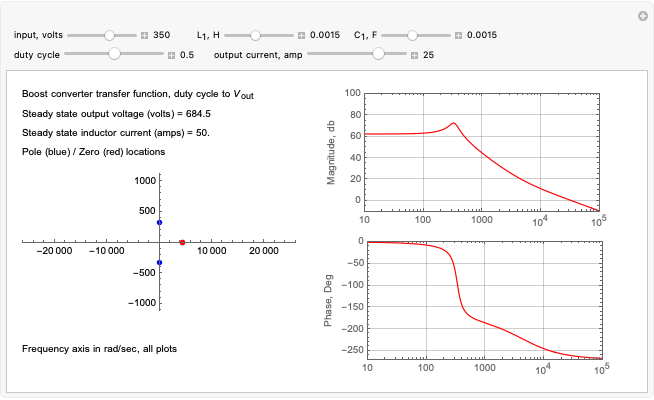
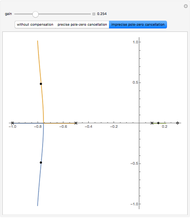
When the transfer function of a system has poles in the right half-plane of the complex numbers, the system is unstable. While it is theoretically possible to design a proportional-derivative (PD) compensator to cancel the poles, in practice is it is difficult to create perfect pole-zero cancellation due to imprecision in the model.
[more]
Contributed by: Hugo Tadashi (March 2011)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation