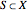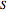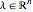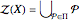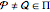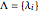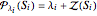Zonotope Construction via Shephard's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
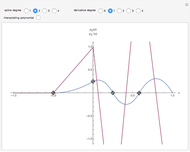
Given  , a set of generators for
, a set of generators for 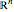 , the zonotope
, the zonotope 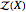 generated by
generated by 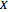 is the convex hull of all vectors of the form
is the convex hull of all vectors of the form 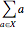 ,; that is,
,; that is, 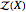 is the Minkowski sum of all segments
is the Minkowski sum of all segments  , where
, where  . Also,
. Also, 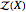 is the shadow of the
is the shadow of the  -dimensional cube
-dimensional cube  via the projection
via the projection 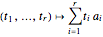 .
.
Contributed by: Lorenzo Dello Schiavo (September 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
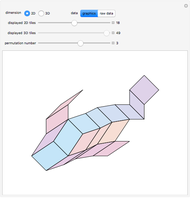
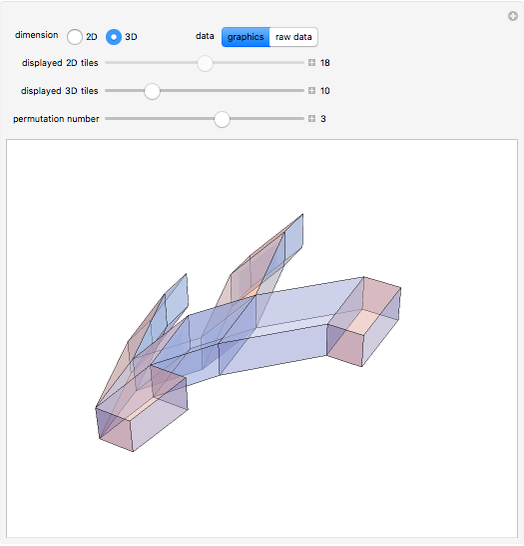
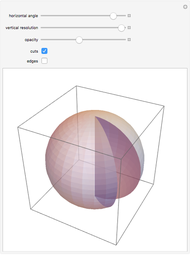
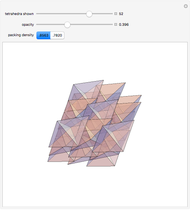
The 3D sample shows inductive construction via Shephard's algorithm of a zonohedron (a 3D zonotope) generated by a set of eight vectors spanning 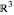 ; the paving results in 49 different parallelepipeds corresponding to the 49 different bases of
; the paving results in 49 different parallelepipeds corresponding to the 49 different bases of 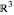 , which may be extracted from the set.
, which may be extracted from the set.
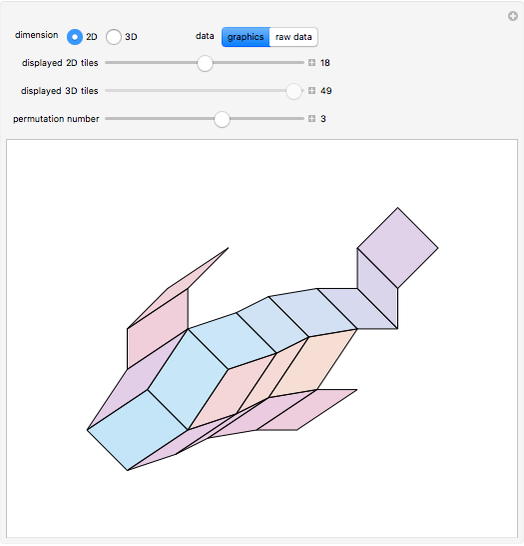
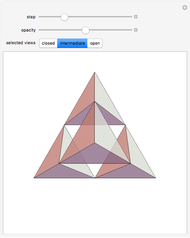
The 2D sample shows an analogous construction of a zonotope generated by a set of nine vectors spanning  ; the paving results in 36 different parallelepipeds.
; the paving results in 36 different parallelepipeds.
Raw data is a matrix representation (by columns) of the parallelepipeds in each paving, i.e. the first  columns of each matrix form a basis
columns of each matrix form a basis  of
of 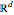 , while the last one is the corresponding vector
, while the last one is the corresponding vector  found via Shephard's algorithm.
found via Shephard's algorithm.
Permutation # allows a permutation the initial vectors' sets (both in 2D and 3D) in six different ways. Since the algorithm is order sensitive, any permutation of these sets produces a different rearrangement of the tiles, which are nonetheless always the same and pave the same zonotope, showing that the latter only depends on its generating set. The recursion property of the algorithm may be deduced by the connectedness of the partial pavings at each step.
Details of the construction and a complete proof of Shephard's theorem may be found in §2.3 of [1].
Reference
[1] C. De Concini and C. Procesi, Topics in Hyperplane Arrangements, Polytopes, and Box Splines, New York: Springer, 2010.
Permanent Citation