A 2011 IMO Tangency Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
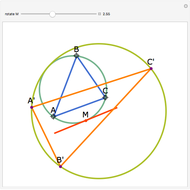
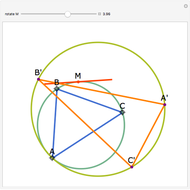
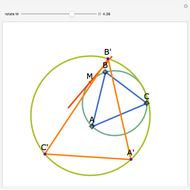
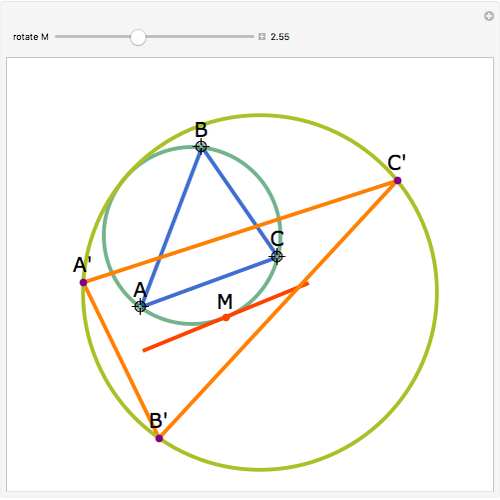
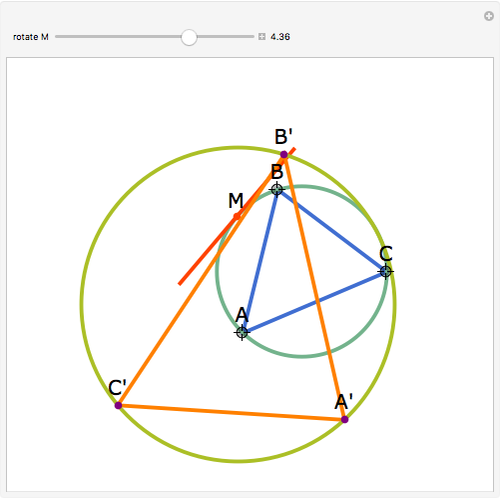
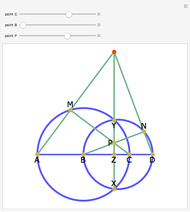
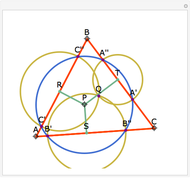
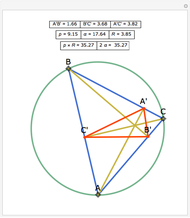
Let 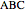 be an acute triangle with circumcircle
be an acute triangle with circumcircle  . Let
. Let 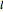 be a tangent line to
be a tangent line to  at the point
at the point 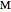 and let
and let 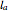 ,
, 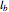 , and
, and 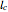 be the lines obtained by reflecting
be the lines obtained by reflecting 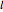 in the lines
in the lines 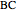 ,
, 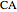 , and
, and 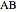 , respectively. Let
, respectively. Let  be the triangle formed by the intersections of
be the triangle formed by the intersections of 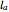 ,
,  , and
, and  . Then the circumcircle of
. Then the circumcircle of 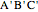 is tangent to the circle
is tangent to the circle  .
.
Contributed by: Jay Warendorff (August 2011)
Open content licensed under CC BY-NC-SA
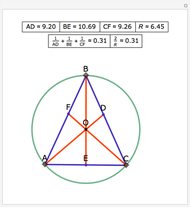
Snapshots
Details
This is problem 6 in the 2011 International Mathematical Olympiad; see International Mathematical Olympiad Problems.
Permanent Citation
"A 2011 IMO Tangency Problem"
http://demonstrations.wolfram.com/A2011IMOTangencyProblem/
Wolfram Demonstrations Project
Published: August 29 2011