1. Nets for Cowley's Dodecarhombus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
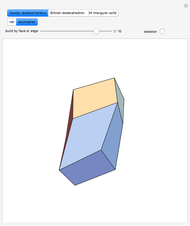
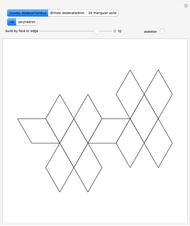
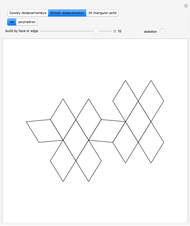
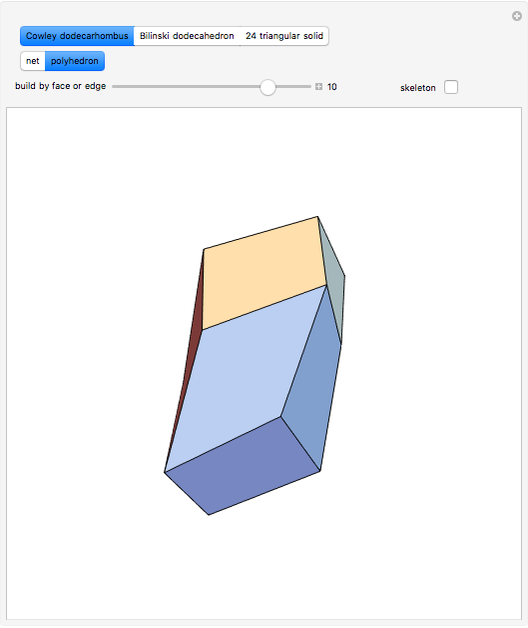
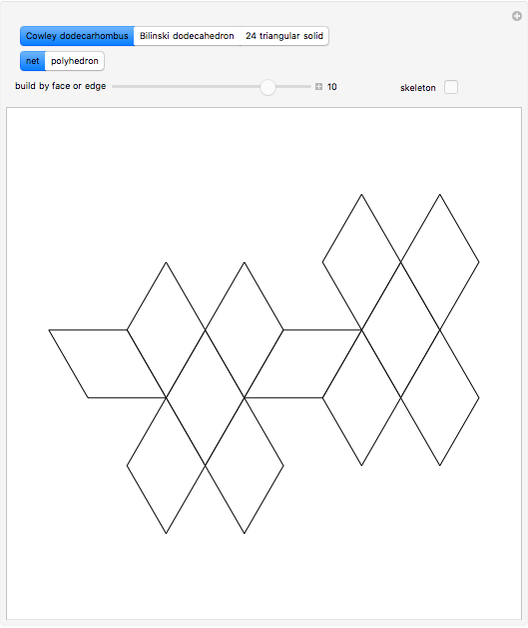
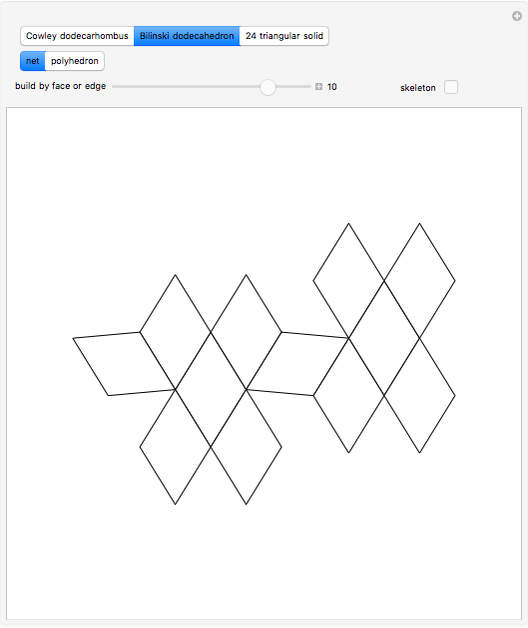
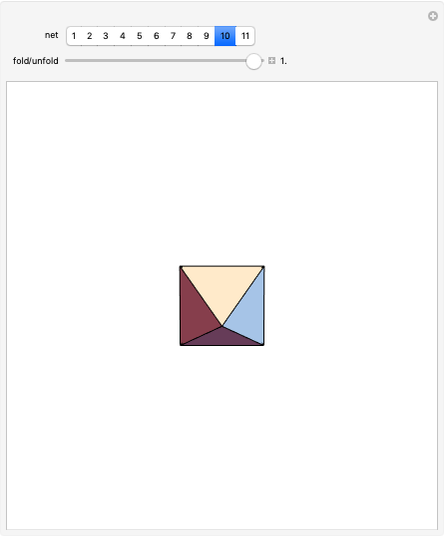
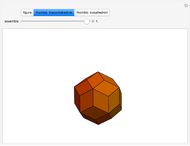
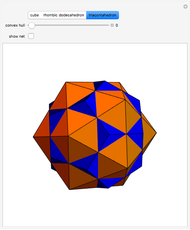
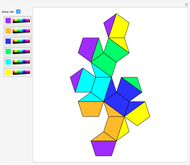
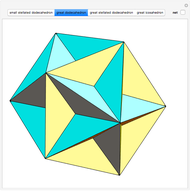
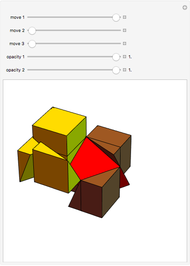
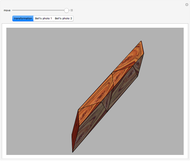
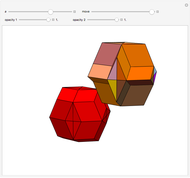
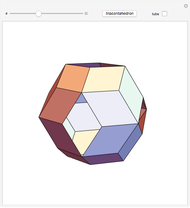
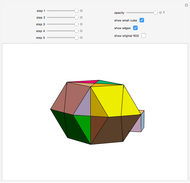
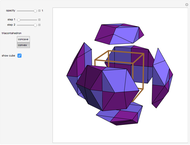
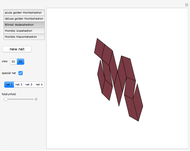
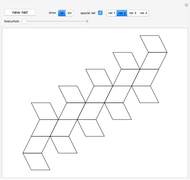
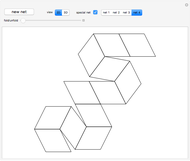
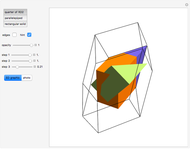
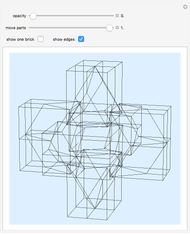
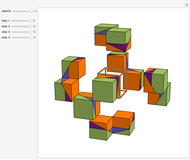
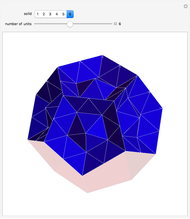
This Demonstration shows that Cowley's net can be folded into a nonconvex solid with nonplanar faces.
[more]
Contributed by: Izidor Hafner and Ed Pegg Jr (March 25)
Open content licensed under CC BY-NC-SA
Details
According to [6, 7] the shape appears in a 1752 book by John Lodge Cowley, labeled as the dodecarhombus [2] and is named after Stanko Bilinski, who rediscovered it in 1960. But the rhombuses of Cowley are 60° degree [3], so the previous statement is not true.
References
[1] "Rombski Poliedri." (Dec 3, 2018) www.logika.si/revija/Stare-revije/revija15-5.pdf.
[2] J. L. Cowley, Geometry Made Easy: A New and Methodical Explanation of the Elemnets [sic] of Geometry, London: Mechell, 1752.
[3] B. Grünbaum. "The Bilinski Dodecahedron, and Assorted Parallelohedra, Zonohedra, Monohedra, Isozonohedra and Otherhedra." (Dec 3, 2018) digital.lib.washington.edu/researchworks/bitstream/handle/1773/15593/Bilinski_dodecahedron.pdf.
[4] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
[5] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York, NY: Springer Berlin Heidelberg, 2018.
[6] Wikipedia. "Bilinski Dodecahedron." (Jan 7, 2019) en.wikipedia.org/wiki/Bilinski_dodecahedron.
[7] G. Hart (2000), "A color-matching dissection of the rhombic enneacontahedron", Symmetry: Culture and Science, 11 (1–4): 183–199, http://www.georgehart.com/dissect-re/dissect-re.htm
Snapshots
Permanent Citation