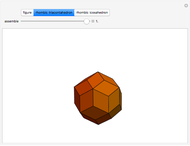
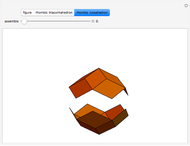
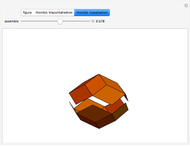
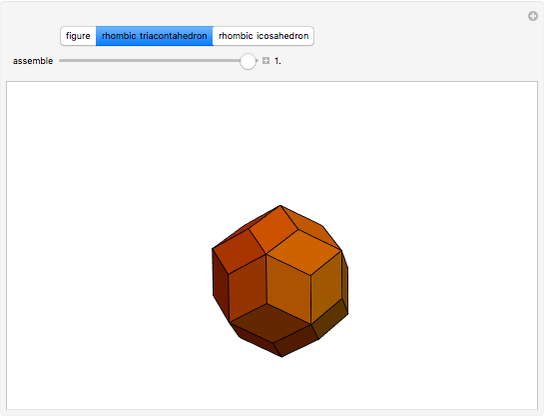
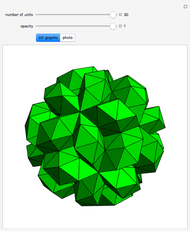
Kepler's Rhombic Triacontahedron and Rhombic Icosahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
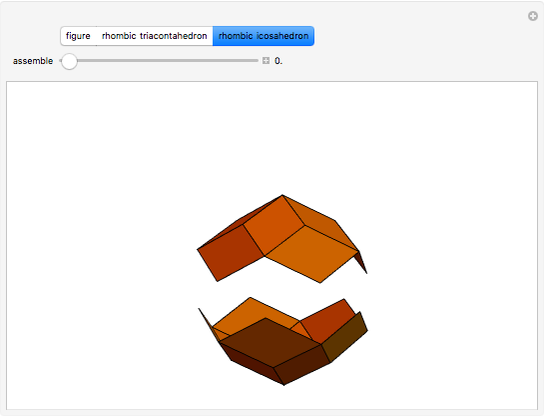
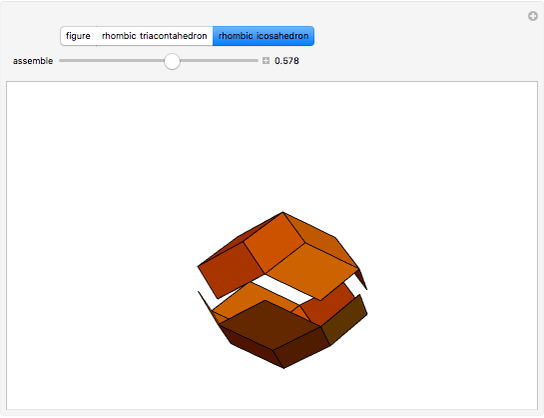
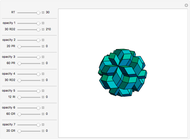
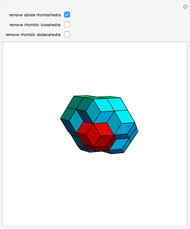
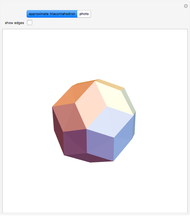
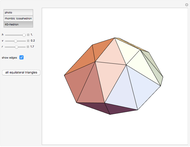
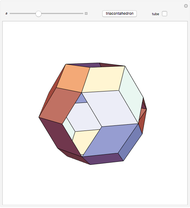
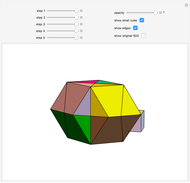
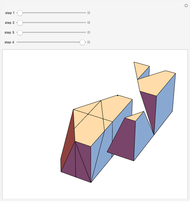
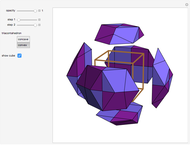
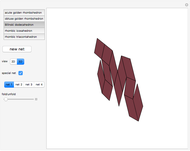
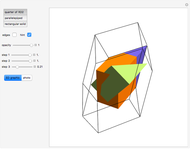
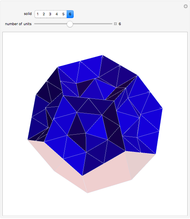
Kepler made a systemic study of polyhedra beyond the ones defined by Archimedes. Among those were the rhombic icosahedron and the rhombic triacontahedron, which he used in Harmonices Mundi.
Contributed by: Izidor Hafner (January 2019)
Open content licensed under CC BY-NC-SA
Details
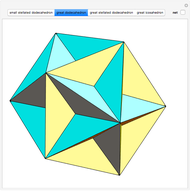
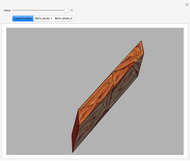
A part of an illustration from Kepler's Harmonices Mundi (taken from [4] for this Demonstration, also [5, p. 79]) suggests that Kepler was aware of the rhombic icosahedron; its discovery is attributed to Fedorov [2, p. 156].
References
[1] B. Grünbaum. "The Bilinski Dodecahedron, and Assorted Parallelohedra, Aonohedra, Monohedra, Isozonohedra and Otherhedra." (Jan 7, 2019) digital.lib.washington.edu/researchworks/bitstream/handle/1773/15593/Bilinski_dodecahedron.pdf.
[2] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
[3] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York, NY: Springer Berlin Heidelberg, 2018.
[4] S. Wolfram. "The Story of Spikey" from Wolfram Blog—A Wolfram Web Resource. (Jan 7, 2019) blog.wolfram.com/2018/12/28/the-story-of-spikey.
[5] J. Kepler, Harmonices Mundi, 1619. (Jan 7, 2019) archive.org/details/ioanniskepplerih00kepl/page/n79.
Snapshots
Permanent Citation