2D Wave Propagation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
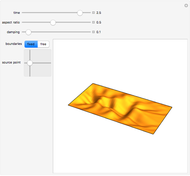
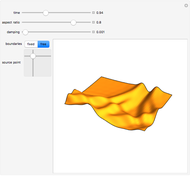
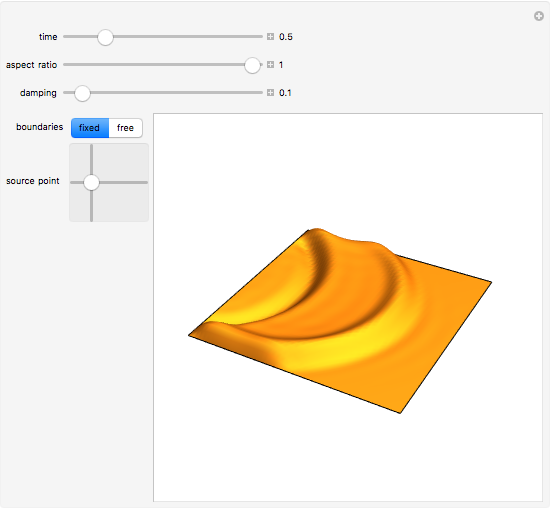
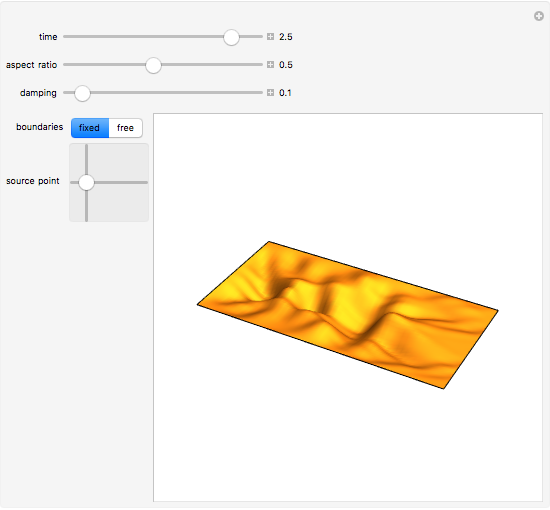
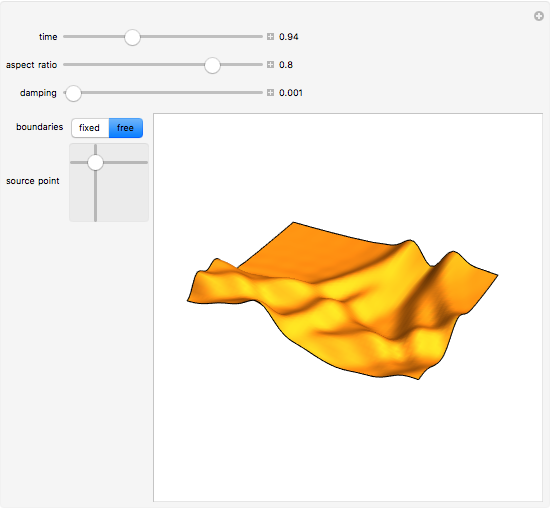
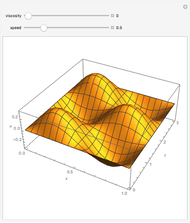
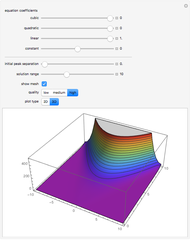
This Demonstration shows the solution of the two-dimensional wave equation subjected to an instantaneous hammer hit centered at the source point location with zero initial displacement and velocity. You can choose free or fixed boundary conditions. A fast and accurate solution was obtained by using the orthogonal function expansion method. By decreasing the aspect ratio, the solution approaches the one-dimensional approximation.
Contributed by: Jason Beaulieu and Brian Vick (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The dimensionless 2D wave equation can be written
 .
.
The fixed boundary conditions are
 ,
,  ,
,  ,
, 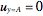 .
.
The free boundary conditions are
 ,
,  ,
, 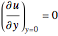 ,
,  .
.
The initial conditions are
 and
and 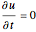 at
at  .
.
Using Fourier analysis, we can transform each forcing function and the differential equation to create a solution in the form of
 ,
,
where  and
and  are the respective eigenfuntions and
are the respective eigenfuntions and  is the transformation of
is the transformation of 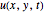 .
.
Permanent Citation