Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

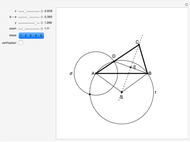
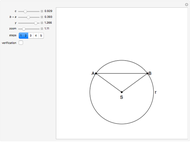
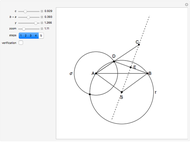
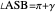30. Construct a Triangle ABC Given the Length of AB, the Angle at C and the Difference of the Other Two Sides

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

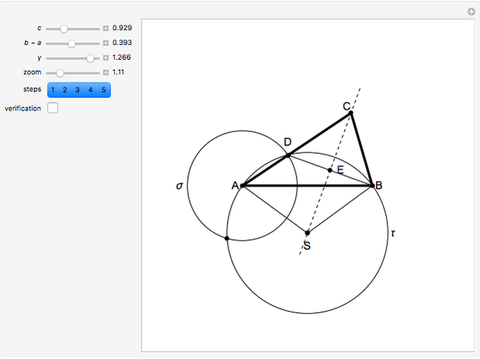
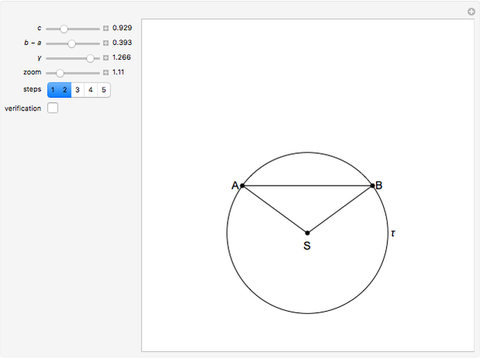
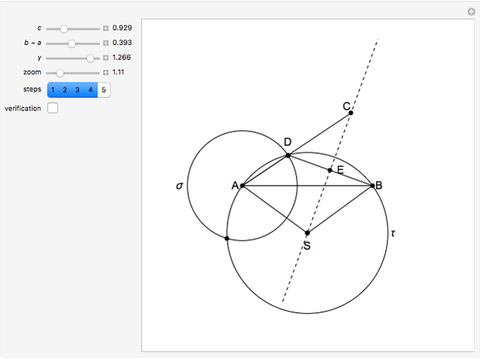
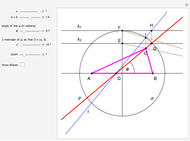
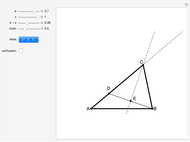
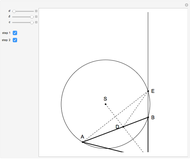
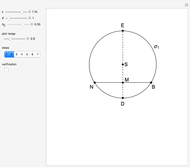
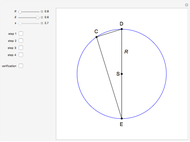
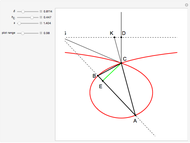
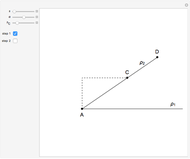
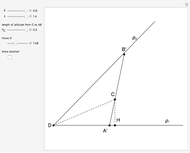
This Demonstration shows how to construct a triangle 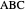given the length of side , the opposite angle at and the difference of the lengths of the other two sides .

[more]

Construction

1. Draw the segment of length .

2. Draw the circle with center so that .

3. Draw the circle with center and radius . Let the circles and meet at .

4. Let the point be the intersection of the ray and the perpendicular bisector of .

5. Then is the required triangle.

Verification

since it is an arc corresponding to the central angle . Since is an isosceles triangle with apex , and .

Thus .

[less]

Contributed by: Izidor Hafner (April 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The problem was posed in [1, section IX, problem 2, solution pp. 291–292] and in [2, problem 2, p. 143].

References

[1] M. Bland, Geometrical Problems Deducible from the First Six Books of Euclid, Arranged and Solved, Cambridge: J. Smith, 1819.

[2] M. Bland and A. Wiegand, Geometrische Aufgaben für Hohëre Lehranstalten, Braunschweig: Schewetschke und Sohn, 1865. babel.hathitrust.org/cgi/pt?id=njp.32101076800687;view=1up;seq=143.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send