Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

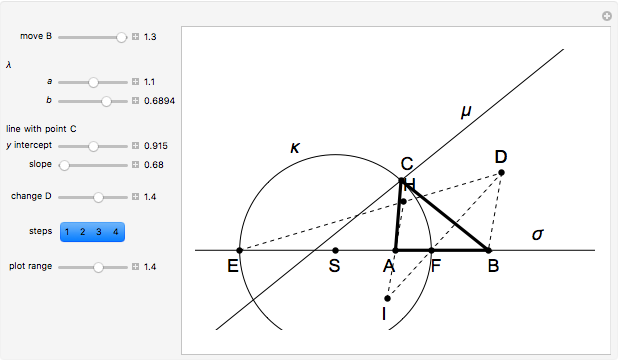
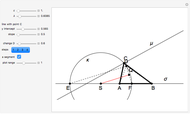
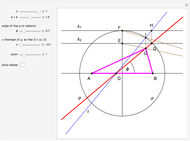
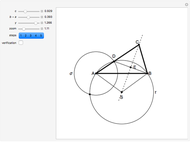
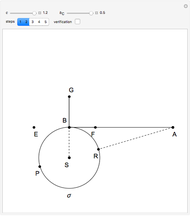
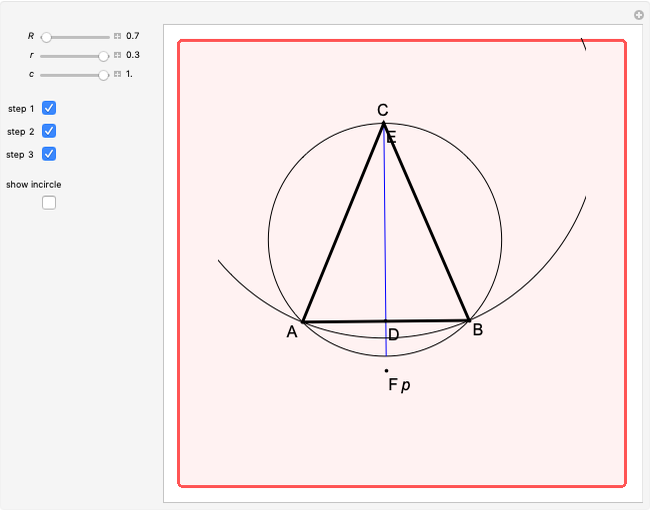
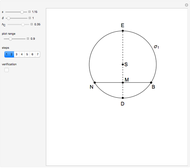
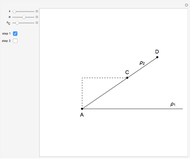
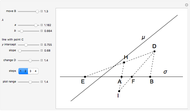
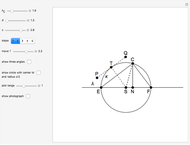
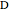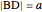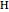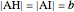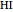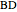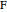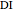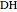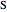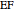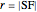32b. Construct a Triangle ABC Given the Length of AB, the Ratio of the Other Two Sides and a Line through C

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration shows the construction of a triangle 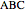given the length of the base 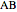, the ratio 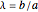of the other two sides and a line containing .

[more]

Construction

1. Draw a line and a line through and .

2. Draw the point such that . Draw the points and so that and is parallel to . Let be the point where and intersect. Let be the point where meets .

3. Let be the midpoint of . Draw the circle with center and radius .

4. The point is an intersection of and .

Verification

The circle is the Apollonius circle of the points and with respect to the ratio .

[less]

Contributed by: Gerd Baron, Izidor Hafner, Marko Razpet and Nada Razpet (August 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

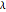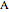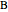An Apollonius circle is the circle defined by the locus of points for which the ratio of the distances from two given points is a fixed number . In this case, the fixed points are and , and .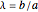

The radius of the Apollonius circle is

if . This depends only on and .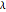

Reference

[1] E. J. Borowski and J. M. Borwein, Collins Dictionary of Mathematics, New York: HarperCollins Publishers, 1989 pp. 21–22.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send