Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

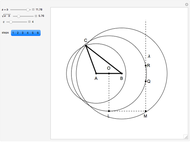
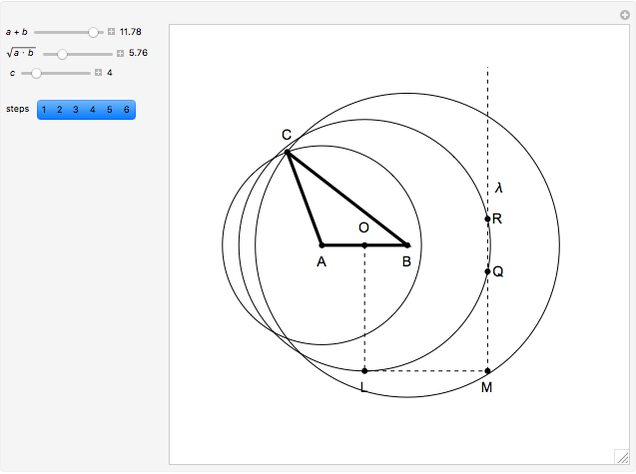
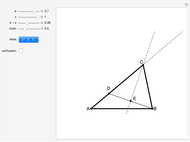
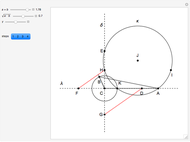
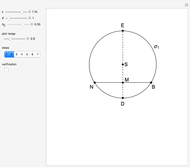
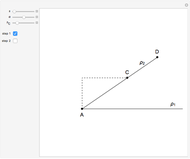
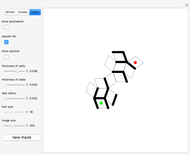
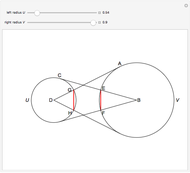
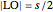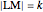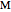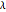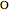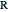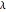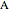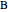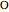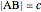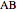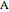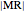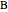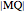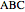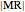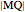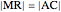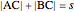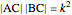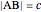34. Construct a Triangle ABC Given the Length of AB and the Sum and Product of the Other Two Sides

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

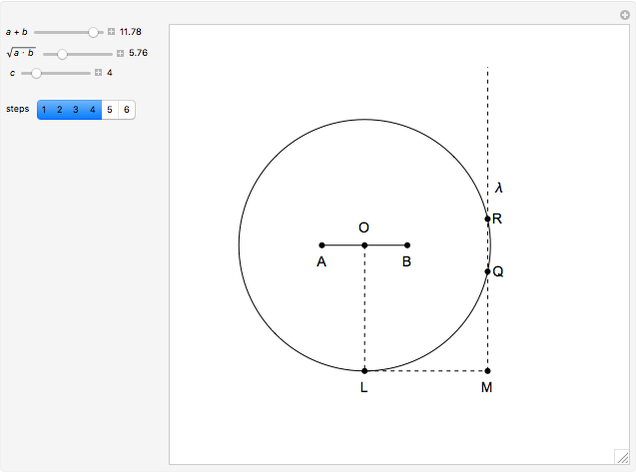
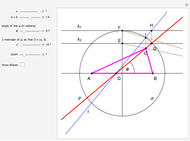
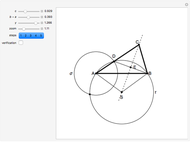
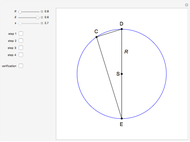
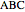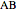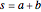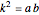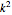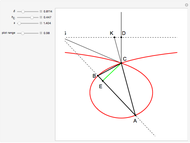
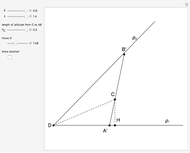
This Demonstration shows how to construct a triangle given the length of the side , the sum of the lengths of the other two sides and their product . The numbers and satisfy the quadratic equation 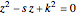. It is solved graphically using Descartes's method for constructing roots of polynomials.

[more]

Construction

1. Draw a vertical line and a horizontal line .

2. Through , draw a vertical line .

3. Draw a circle with center and radius . Let and be the points of intersection of the circle with .

4. Draw points and on a horizontal line through such that and is the midpoint of .

5. Let the point be the intersection of the circle with center and radius and the circle with center and radius .

6. The triangle satisfies the given conditions.

Verification

According to Descartes's method, and are the solutions of the quadratic equation, but and , so and . By step 5, .

[less]

Contributed by: Izidor Hafner and Marko Razpet (September 2018)
Open content licensed under CC BY-NC-SA

Details

Let 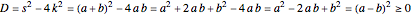. Thus 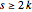or 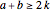. The triangle inequality is 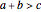, which is 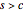. Suppose 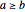; the triangle inequality 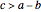implies .

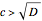Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send