A Continuous Analog of the 1D Thue-Morse Sequence

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
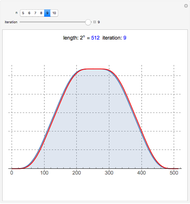
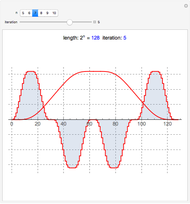
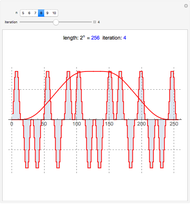
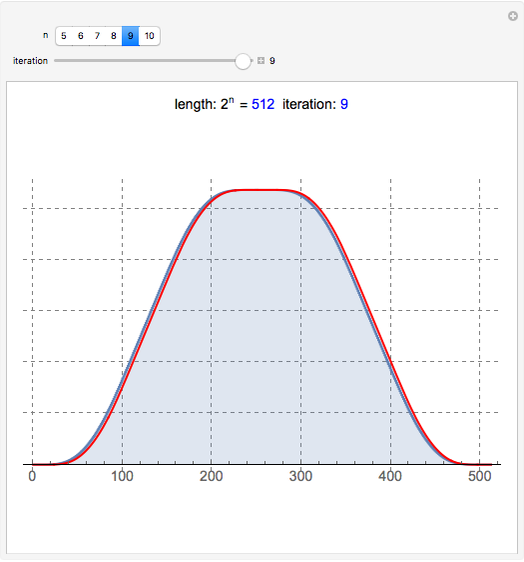
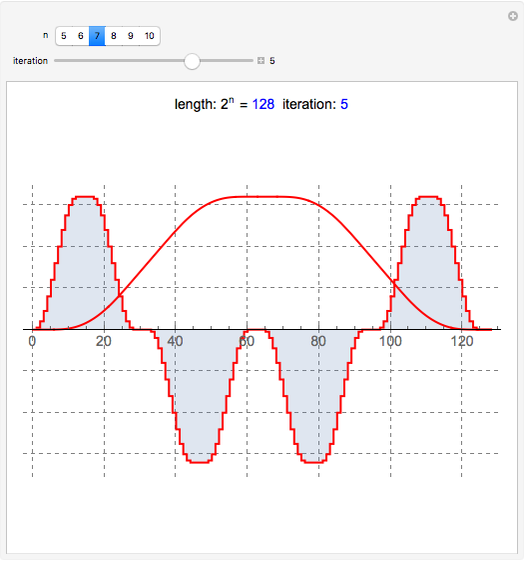
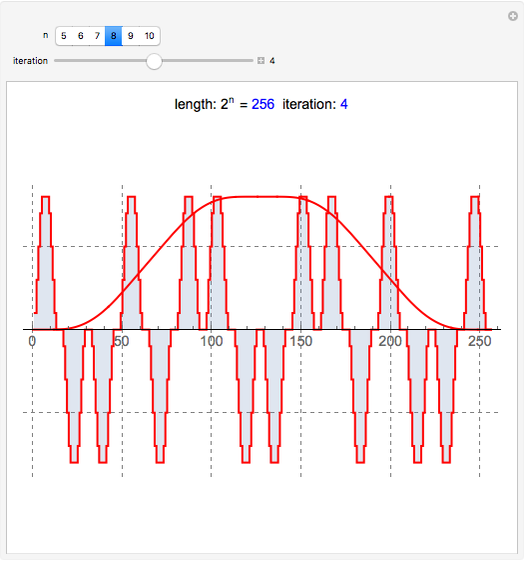
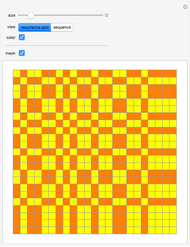
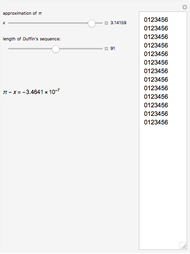
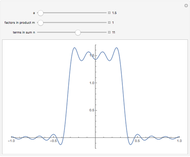
This Demonstration shows a connection [1, 2] between the  Thue–Morse (Prouhet–Thue–Morse) sequence and the infinitely differentiable
Thue–Morse (Prouhet–Thue–Morse) sequence and the infinitely differentiable  or
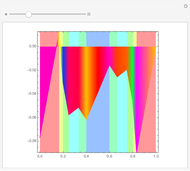
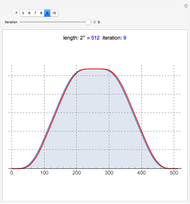
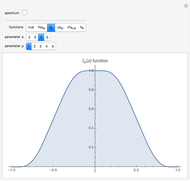
or  atomic functions. By definition, an atomic function is a finite solution of a functional differential equation (FDE) of advanced type, such as
atomic functions. By definition, an atomic function is a finite solution of a functional differential equation (FDE) of advanced type, such as  , where
, where  and
and  is a linear differential operator with constant coefficients. The simplest example of such an FDE is
is a linear differential operator with constant coefficients. The simplest example of such an FDE is  , with
, with  . Its
. Its  solution is called the
solution is called the  (or
(or  ) function with support
) function with support  .
.
Contributed by: Oleg Kravchenko (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] W. Hilberg, S. Wolf. "Korrelationsermittlung durch Stapeln von Impulsen," patent DE 19818694 A1, 1999. www.google.com/patents/DE19818694A1?cl=de.
[2] W. Hilberg, V. F. Kravchenko, O. V. Kravchenko, and Y. Y. Konovalov, "Atomic Functions and Generalized Thue–Morse Sequence in Digital Signal and Image Processing," International Kharkov Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW) 2013, Kharkiv, Ukraine: IEEE 2013. doi:10.1109/MSMW.2013.6621989.
[3] Technische Universität Darmstadt. "Wolfgang Hilberg." (Jan 12, 2015) www.tu-darmstadt.de/universitaet/selbstverstaendnis/profil_geschichte/persoenlichkeiten/thema_perso_k6.en.jsp.
[4] Wikipedia. "Wolfgang Hilberg." (Jan 12, 2015)de.wikipedia.org/wiki/Wolfgang_Hilberg.
[5] W. Hilberg. "Prof. em. Dr. Ing. Wolfgang Hilberg." (Jan 12, 2015) www.hilberg-wolfgang.de.
[6] Atomic Functions. (Jan 12, 2015) atomic-functions.ru/en.
Permanent Citation