Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Approximate Solutions of a Functional Differential Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

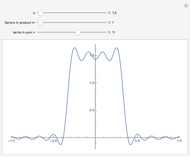
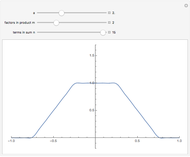
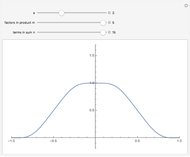
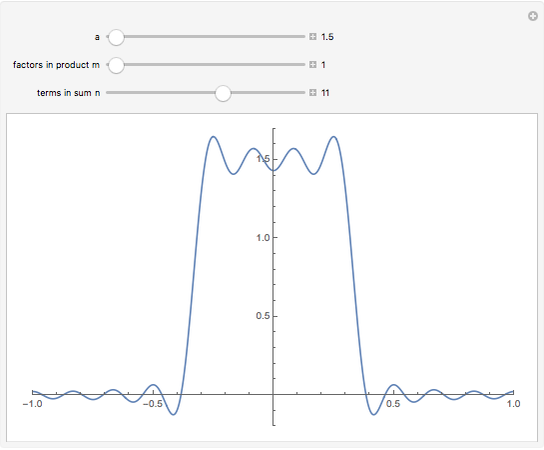
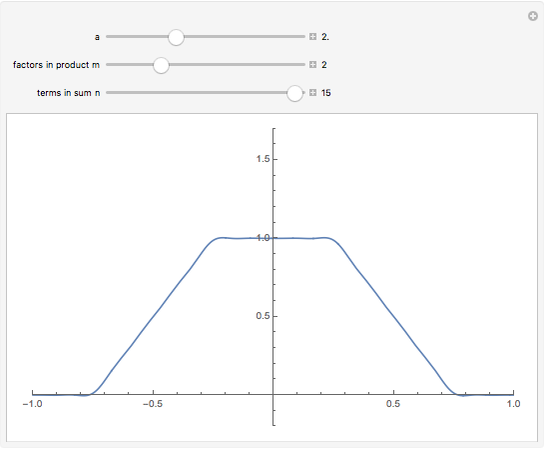
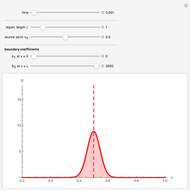
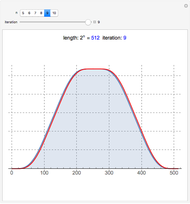
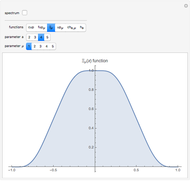
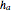This Demonstration shows Fourier approximations of the solution of the functional differential equation of advanced type, , where and the support of is . The Fourier approximation is .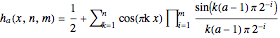

Contributed by: Oleg Kravchenko (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References


[1] V. M. Kolodyazhny and V. A. Rvachov, "Atomic Functions: Generalization to the Multivariable Case and Promising Applications," Cybernetics and Systems Analysis, 43(6), 2007 pp. 893–911.

[2] V. F. Kravchenko, H. Perez-Meana, and V. I. Ponomaryov, Adaptive Digital Processing of Multidimensional Signals with Applications, Moscow: Fizmatlit, 2009.

[3] E. Nakai and T. Yoneda, "Construction of Solutions for the Initial Value Problem of a Functional-Differential Equation of Advanced Type," Aequationes Mathematicae, 77(3), 2009 pp. 259–272.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send