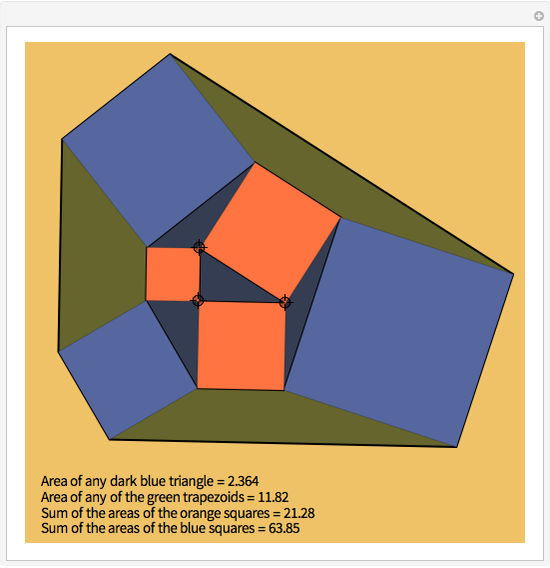
A Generalization of Cross's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
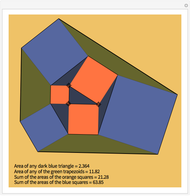
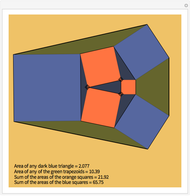
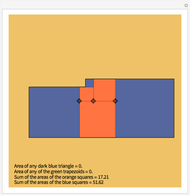
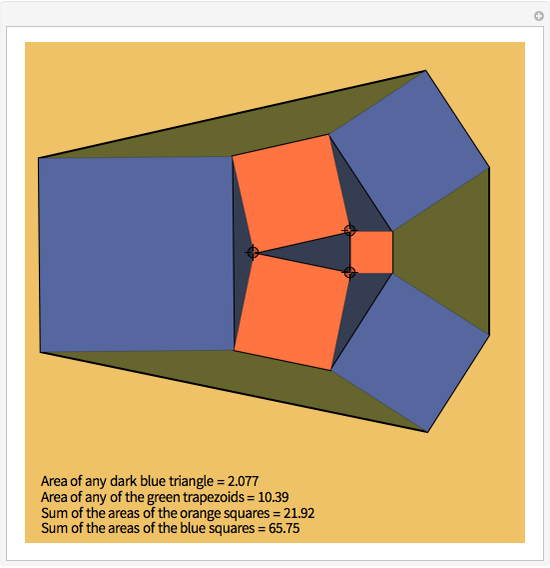
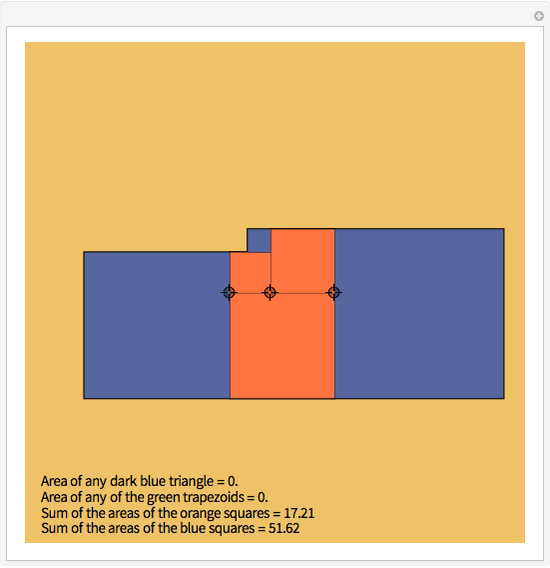
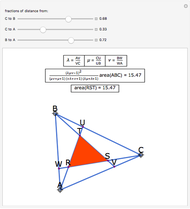
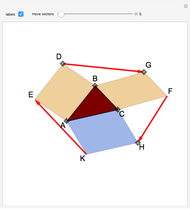
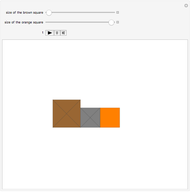
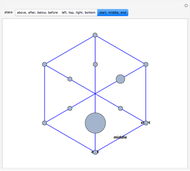
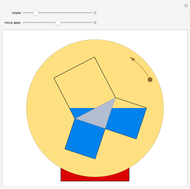
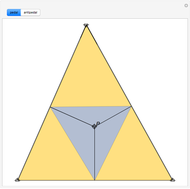
Cross's theorem (apparently named in the United Kingdom after a 14-year-old boy who "discovered" it) states that the areas of all triangles in the above arrangement are equal, a fact that is easily proved applying basic principles. This Demonstration shows that, in the further building of squares on the sides of triangles, each of the green trapezioids has equal area and that amount is equal to five times the area of the central triangle (or indeed any other triangle). Also, the sum of the areas of the blue squares is equal to three times the sum of the areas of the orange squares.
Contributed by: Jaime Rangel-Mondragon (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"A Generalization of Cross's Theorem"
http://demonstrations.wolfram.com/AGeneralizationOfCrosssTheorem/
Wolfram Demonstrations Project
Published: August 29 2011