A Model for Fermi-Dirac Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
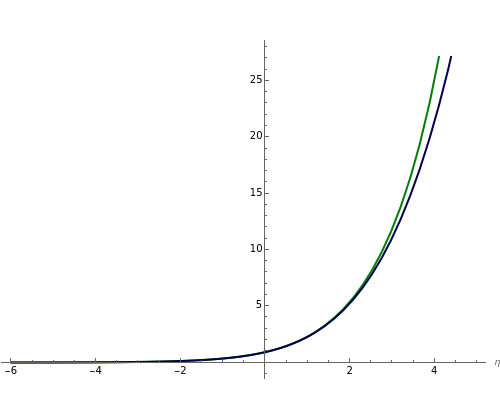
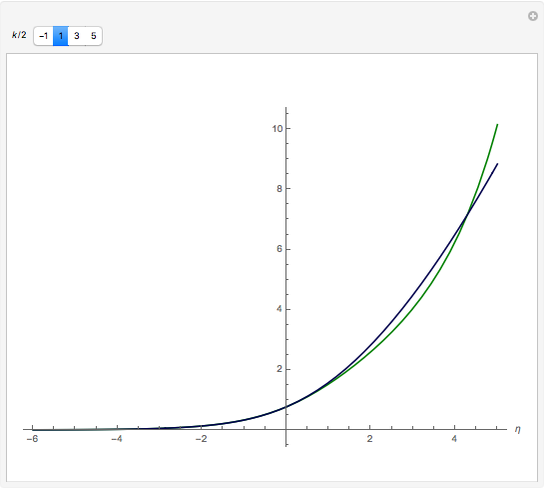
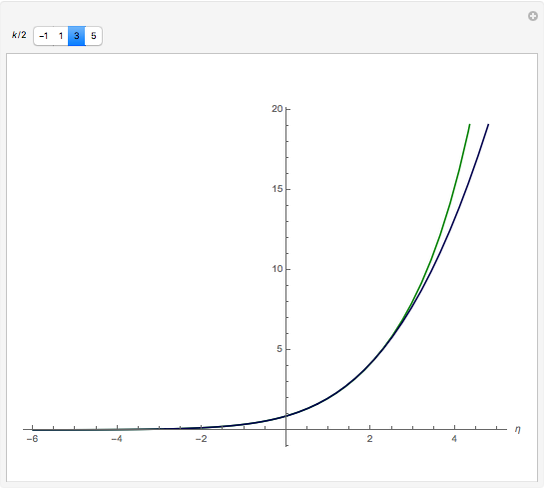
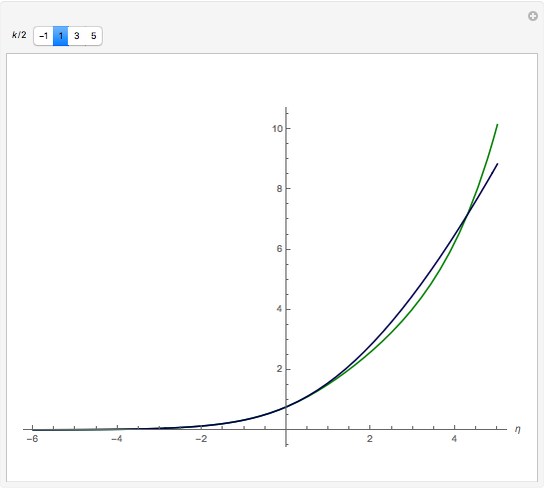
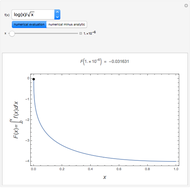
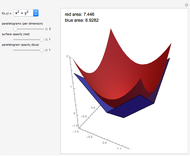
Fermi–Dirac integrals arise in calculating pressure and density in degenerate matter, such as neutron stars; they also occur in the electronic density of semiconductors. A (semi-)closed form was not known until 1995, when Howard Lee noticed the application of the integral form of polylogarithms. We developed an alternative expression,  (plotted here), using an exponential model that is accurate for
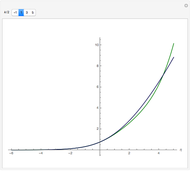
(plotted here), using an exponential model that is accurate for  (arXiv:0909.3653v5 [math.GM]). Here we compare the model, in green, with the polylogarithm expression, in blue, for Fermi–Dirac integrals half-integer order
(arXiv:0909.3653v5 [math.GM]). Here we compare the model, in green, with the polylogarithm expression, in blue, for Fermi–Dirac integrals half-integer order  , with
, with  (orders commonly used in astrophysics and semiconductors).
(orders commonly used in astrophysics and semiconductors).
Contributed by: Michael Morales (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Written in terms of polylogarithms, the (normalized) Fermi–Dirac integral is [2]  .
Meanwhile, the model is found to be
.
Meanwhile, the model is found to be  ,
where
,
where  is a function written in terms of the Lambert function (see [1] and references therein).
is a function written in terms of the Lambert function (see [1] and references therein).
References
[1] M. H. Lee, "Polylogarithmic Analysis of Chemical Potential and Fluctuations in a d-Dimensional Free Fermi Gas at Low Temperatures," Journal of Mathematical Physics, 36, 1995 pp. 1217–1231.
[2] M. Morales, "Fermi-Dirac Integrals in Terms of Zeta Functions," arXiv:0909.3653v5 [math.GM].
Permanent Citation