A Path through the Lattice Points in a Quadrant

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
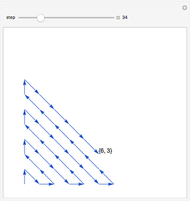
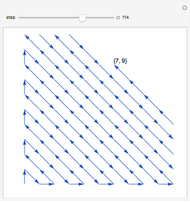
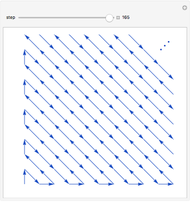
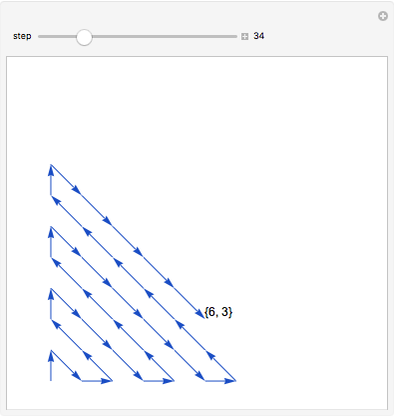
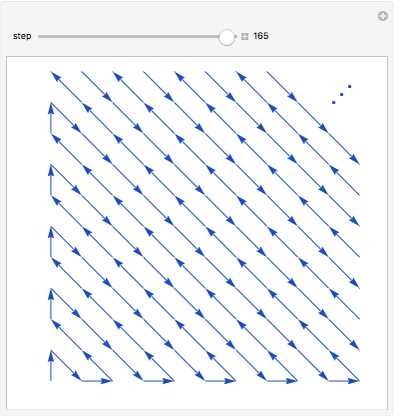
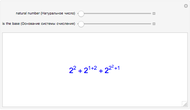
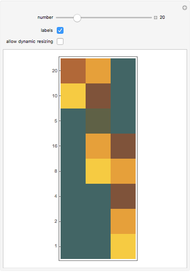
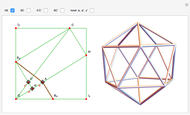
Let  be the set of positive integers. The set of lattice points in the first quadrant is the set
be the set of positive integers. The set of lattice points in the first quadrant is the set  , where both coordinates are positive integers. Even though
, where both coordinates are positive integers. Even though  is two-dimensional, it is possible to set up a one-to-one correspondence between
is two-dimensional, it is possible to set up a one-to-one correspondence between  and
and  , as shown in the picture.
, as shown in the picture.
Contributed by: George Beck (November 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A set is enumerable (or denumerable or countable or listable) if it can be written as  . In other words, there is a one-to-one correspondence between the set and the positive integers.
. In other words, there is a one-to-one correspondence between the set and the positive integers.
When there is a one-to-one correspondence between two sets  and
and  , the sets are said to be equipotent (or equinumerous or equipollent or of the same cardinality), which is denoted by
, the sets are said to be equipotent (or equinumerous or equipollent or of the same cardinality), which is denoted by  . The Demonstration shows that
. The Demonstration shows that  .
.
Let  be the set of integers. The mapping that matches
be the set of integers. The mapping that matches  with the
with the  term of the sequence
term of the sequence  is a one-to-one correspondence, so
is a one-to-one correspondence, so  .
.
Use square paper to draw pictures showing that  and
and  . In other words, for
. In other words, for  draw a path that passes through each lattice point above the
draw a path that passes through each lattice point above the  axis exactly once. The path does not have to be connected. Similarly, for
axis exactly once. The path does not have to be connected. Similarly, for  , find a path that passes through every lattice point in the plane exactly once.
, find a path that passes through every lattice point in the plane exactly once.
It is not true that every infinite set is countable. For example, neither the real numbers  nor the complex numbers
nor the complex numbers  are countable (but
are countable (but  ).
).
Permanent Citation