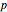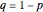Details

Donald Knuth presented and analyzed this problem in [1]. It is also studied in problem 8 of [2]; our Demonstration is based on this book.

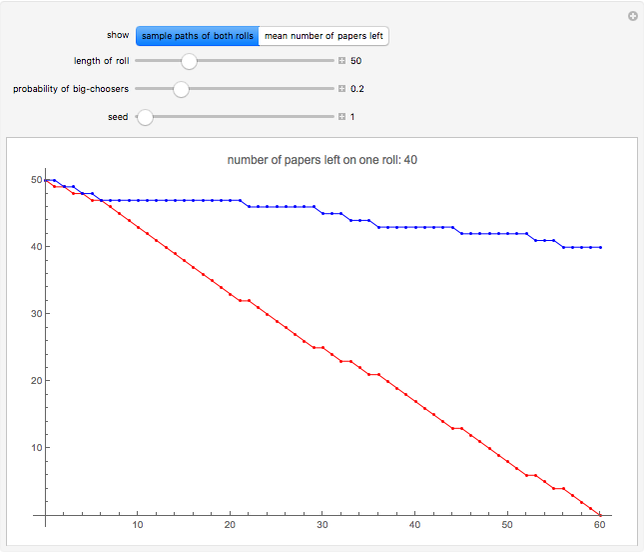
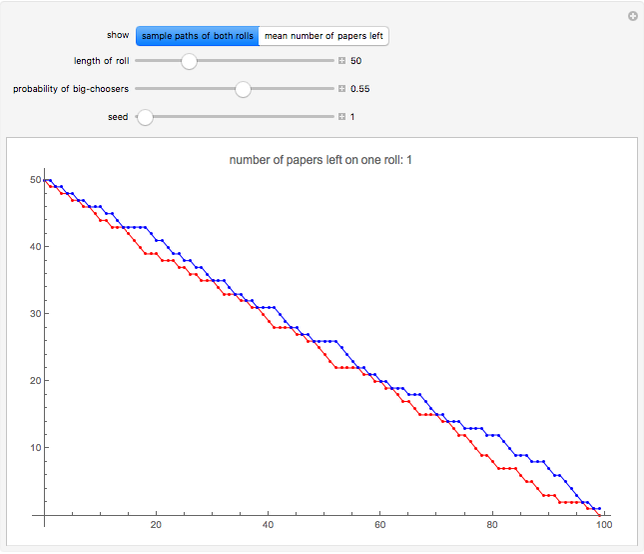
The first snapshot shows that when the probability of a big-chooser is small, most people use the smaller roll so that when it runs out, the other roll contains lots of paper. The second snapshot shows that when the probability of a big-chooser is greater than 0.5, most people use the bigger roll, so that the sizes of the rolls stay close to each other.

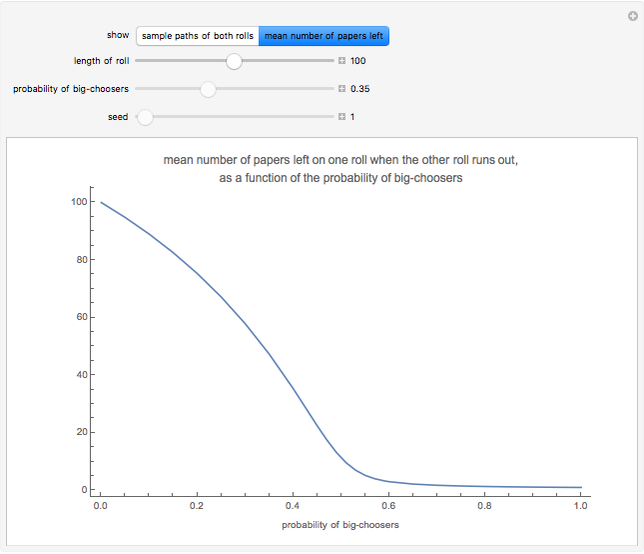
The third snapshot shows the mean number of papers left on one roll when the other roll runs out. The curve shows how this number depends on the probability of big-choosers. We can see a dramatic change in the nature of the curve: when the probability of big-choosers increases from 0 to 0.5, the mean value steadily decreases, but when the probability of big-choosers increases from 0.5, the mean value stays very small. If the probability of big-choosers is, say, 0.4, then on average about 35 papers are left on the other roll, if the rolls initially contain 100 papers.

To calculate the mean value, Nahin develops recursive formulas. They are easy to implement with Mathematica.

References

[1] D. Knuth, "The Toilet Paper Problem," American Mathematical Monthly, 91(8), 1984 pp. 465–470.

[2] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.