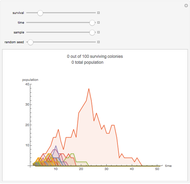
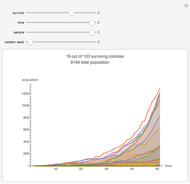
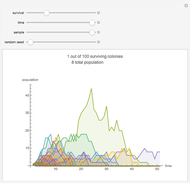
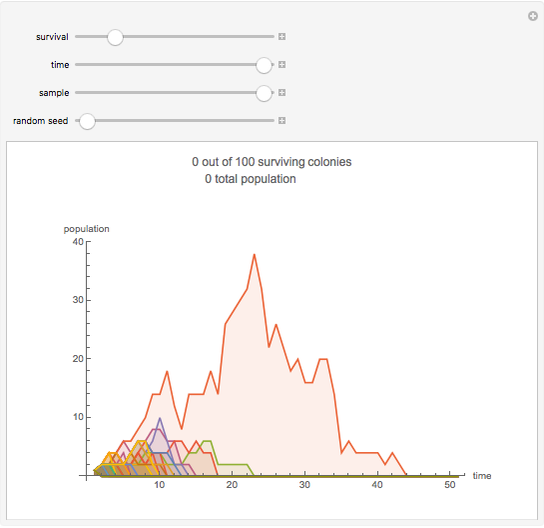
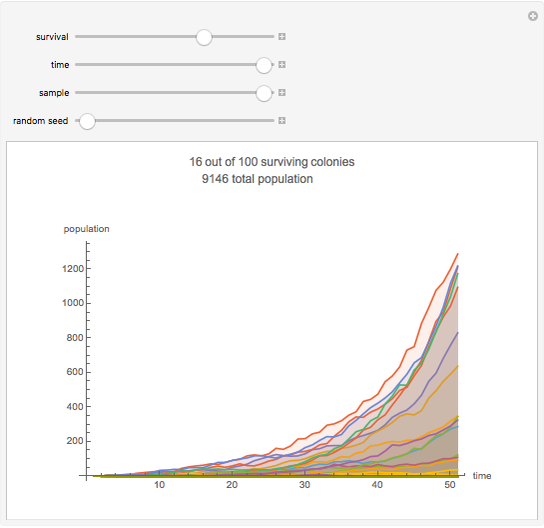
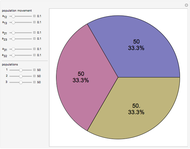
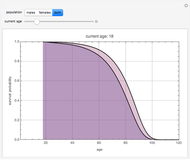
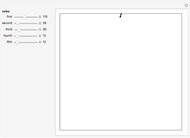
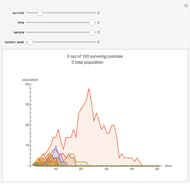
This stylized amoeba problem is a classic illustration of a random process. Each sample colony starts from a single parent amoeba. At each time step, each living amoeba either survives to split into two or dies out, with a constant survival chance. A colony dies out if all its members—daughters of one original parent—die out. For different probabilities of survival, times, and starting sample sizes, the population history of each colony is shown, along with the number of surviving colonies and the total number of surviving individuals.
For individual survival chances well below half, all colonies will frequently die out in finite time.
For high survival chances, many colonies will still die out, but the most successful will grow exponentially, and total population rises as a result.
Larger samples will show more outlier survivors. At short time scales, chance dominates the fate of each colony.
Generalizations of the problem can involve the possibility of more than one daughter cell at each generation, or a link between survival probability and existing population level (to model resource depletion, for example).
The problem can also be thought of as modeling the consequences of a series of double or nothing bets—note how much of the eventual "population" belongs to the most successful colonies.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
