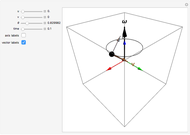
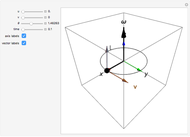
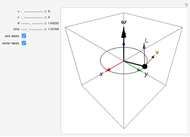
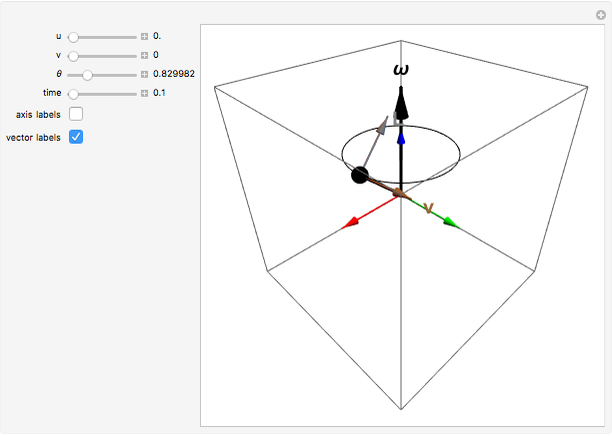
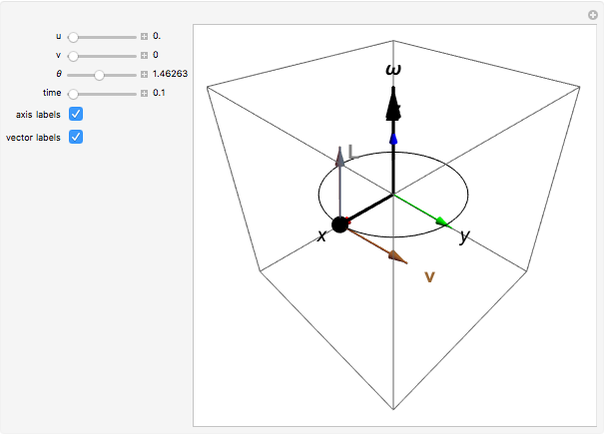
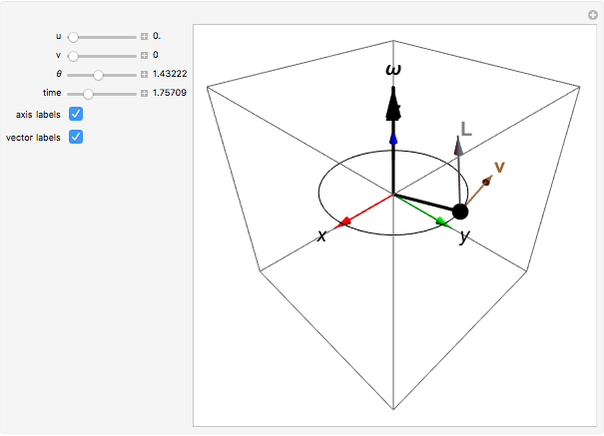
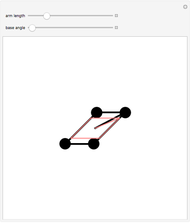
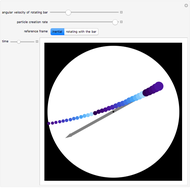
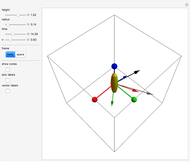
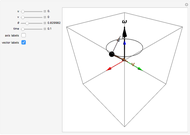
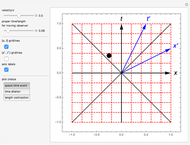
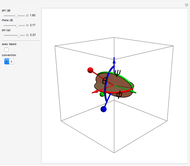
Applying a torque to a particle about a given axis imparts an angular momentum that is not necessarily along the same axis. This is illustrated in this Demonstration for a particle of unit mass. You can vary the initial particle position and the angular velocity vector . The position vector (indicated by the black sphere), the velocity , and the angular momentum all rotate as a function of time about the axis .