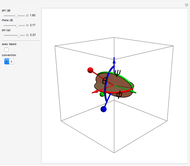
Free Precession of a Rotating Rigid Body

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
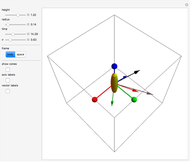
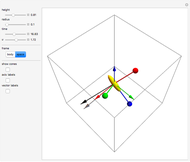
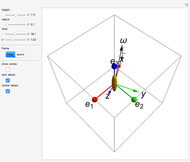
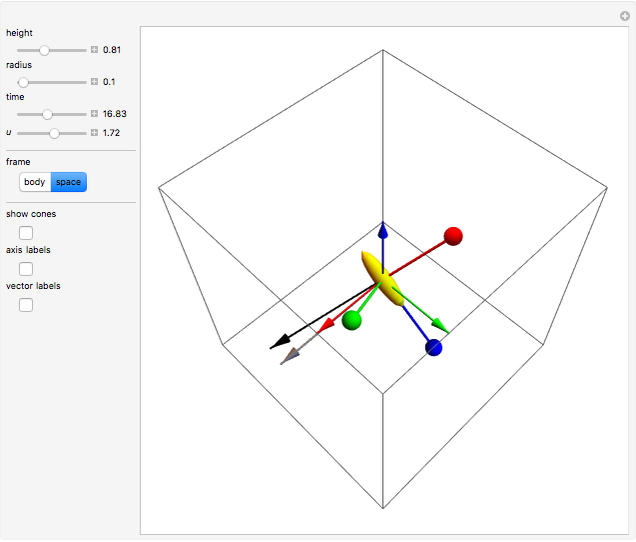
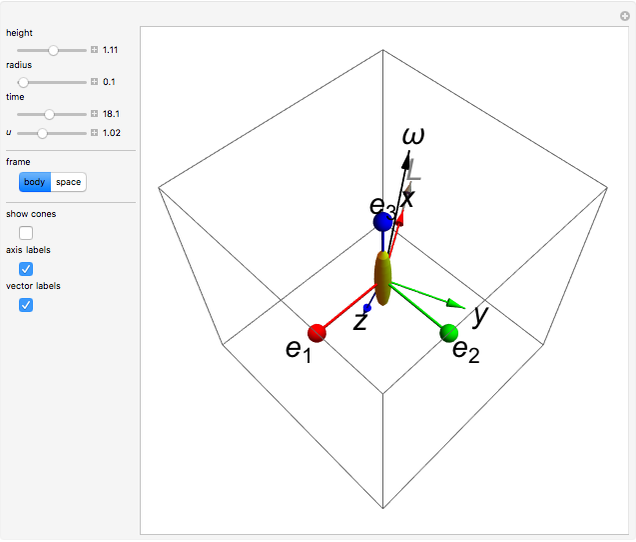
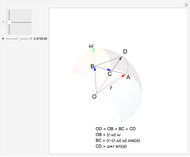
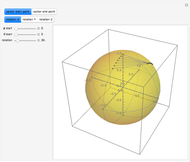
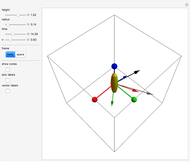
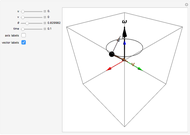
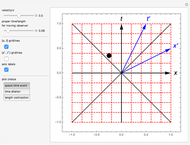
The free precession of a rotating rigid body is a classic application of Euler's equations. Since the precession is free, there is no torque, and the angular momentum is constant in the space frame. In the body frame, however, the body axes 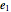 ,
, 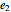 ,
, 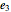 (indicated by the red, green, and blue spheres) are fixed, and the angular momentum
(indicated by the red, green, and blue spheres) are fixed, and the angular momentum  and space axes
and space axes 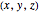 (indicated by the red, green, and blue arrows) will change with time. For an axisymmetric ellipsoid, the angular velocity
(indicated by the red, green, and blue arrows) will change with time. For an axisymmetric ellipsoid, the angular velocity 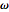 and the angular momentum
and the angular momentum  precess about the symmetry axis
precess about the symmetry axis 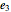 . This precession can be visualized by the rotation of a space cone (centered about
. This precession can be visualized by the rotation of a space cone (centered about  ) around the body cone (centered about
) around the body cone (centered about 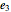 ), with the angular velocity
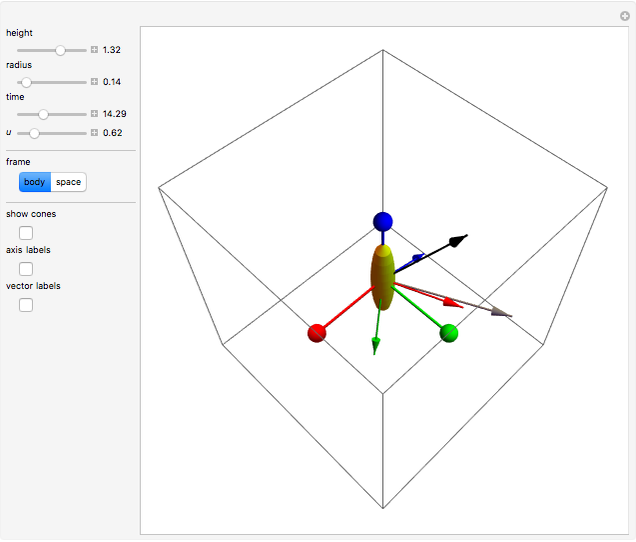
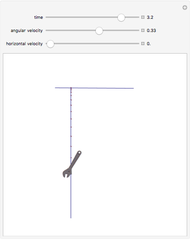
), with the angular velocity 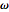 at their point of contact. This Demonstration shows the free precession as a function of time in both the body and space frames. The body's height and radius can be varied, as can the initial angular velocity
at their point of contact. This Demonstration shows the free precession as a function of time in both the body and space frames. The body's height and radius can be varied, as can the initial angular velocity 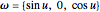 .
.
Contributed by: Frederick W. Strauch (October 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Euler's equations for a rotating rigid body can be exactly solved for the free motion (with zero torque) of an axisymmetric body, with principal moments of inertia  . These give the angular velocity
. These give the angular velocity 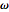 and angular momentum
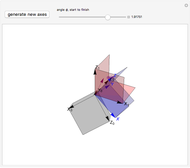
and angular momentum  in the body frame, and will exhibit free precession if the angular velocity is not initially along one of the symmetry axes. The body frame and space frame can be related by a product of two rotation matrices. This is used to transform
in the body frame, and will exhibit free precession if the angular velocity is not initially along one of the symmetry axes. The body frame and space frame can be related by a product of two rotation matrices. This is used to transform 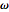 ,
,  , and the space and body axes
, and the space and body axes 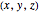 and
and 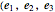 ), and to visualize their dynamics as a function of time. In the body frame, both
), and to visualize their dynamics as a function of time. In the body frame, both 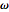 and
and  precess about
precess about 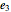 , while in the space frame,
, while in the space frame, 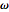 and
and 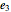 precess about
precess about  .
.
The solution to Euler's equations can be found in the following references. For more information, see the Wikipedia entries for "Euler's equations (rigid body dynamics)" and "Precession".
References
[1] J. R. Taylor, "Rotational Motion of Rigid Bodies," Classical Mechanics, Herndon, VA: University Science Books, 2005 pp. 367–416.
[2] S. T. Thornton and J. B. Marion, "Dynamics of Rigid Bodies," Classical Dynamics of Particles and Systems, Pacific Grove, CA: Brooks/Cole, 2004 pp. 411–467.
Permanent Citation