Archimedes's Method for Determining the Area of a Circle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
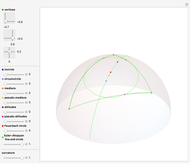
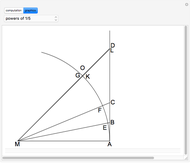
This Demonstration shows how Archimedes determined the area of a circle.
Contributed by: Tomas Garza (March 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
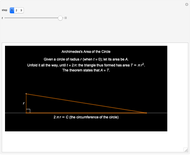
Almost 23 centuries ago, Archimedes determined the area of a circle in terms of  , its circumference. This was a remarkable feat, especially since this was an exact result, relying only on logical arguments and not involving the calculation of the numerical value of
, its circumference. This was a remarkable feat, especially since this was an exact result, relying only on logical arguments and not involving the calculation of the numerical value of  . A detailed description of the problem and Archimedes's reasoning appears in Dunham [1].
. A detailed description of the problem and Archimedes's reasoning appears in Dunham [1].
The result states that the area  of a circle of radius
of a circle of radius  is equal to the area
is equal to the area  of a right-angle triangle, with one side of length
of a right-angle triangle, with one side of length  and the other the circumference of the circle.
and the other the circumference of the circle.
Two basic facts are used to establish the result.
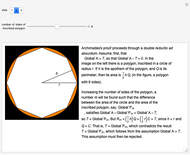
1. The area of a regular polygon with apothem  and perimeter
and perimeter  is
is  . (An apothem of a regular polygon is a line segment or the distance from the center to the midpoint of a side.)
. (An apothem of a regular polygon is a line segment or the distance from the center to the midpoint of a side.)
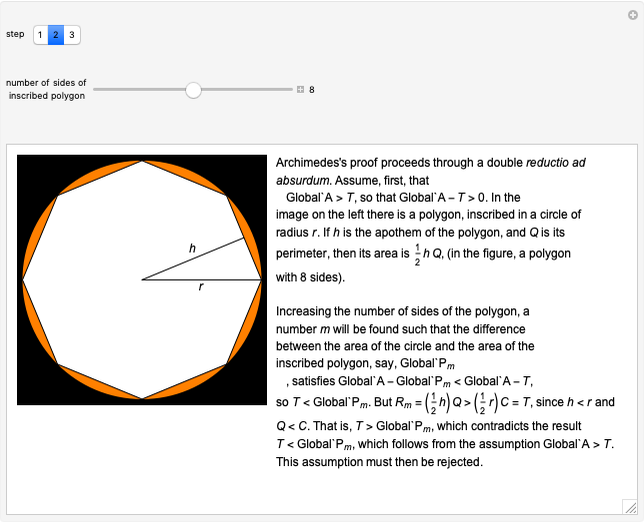
2. The essence of the method of exhaustion: given a preassigned area, no matter how small, one can find an inscribed (or circumscribed) regular polygon for which the difference between the circle's area and the polygon's is less than this preassigned amount [1].
Reference
[1] W. Dunham, Journey through Genius: The Great Theorems of Mathematics, New York: Penguin Books, 1991, pp. 90–92.
Permanent Citation