Euler's Estimate of Pi

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
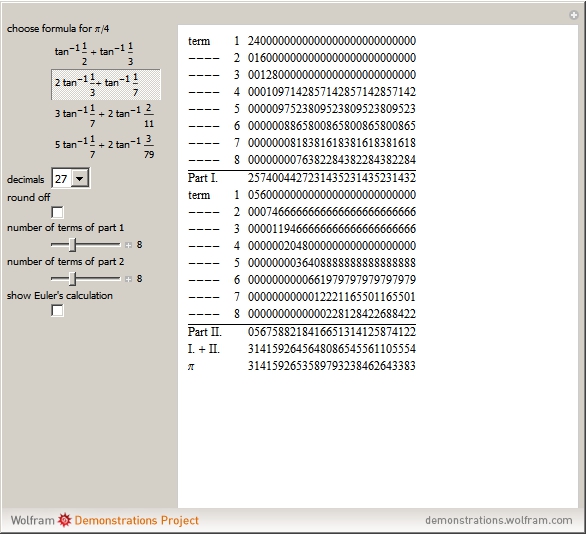
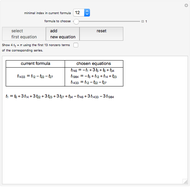
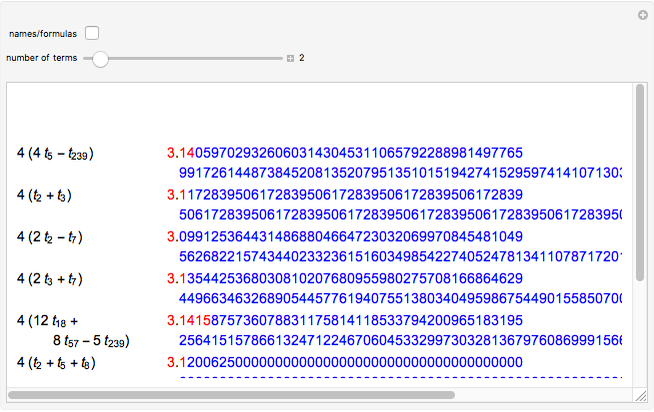
In [1] Euler derived the formula  . He claimed that his formula was better for calculation than the Leibniz–Gregory formula
. He claimed that his formula was better for calculation than the Leibniz–Gregory formula  , since for
, since for  , the factor
, the factor  in the series has values
in the series has values  , which are simpler to calculate with. He illustrated this with the formula
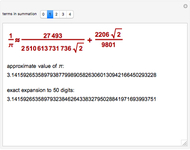
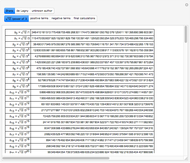
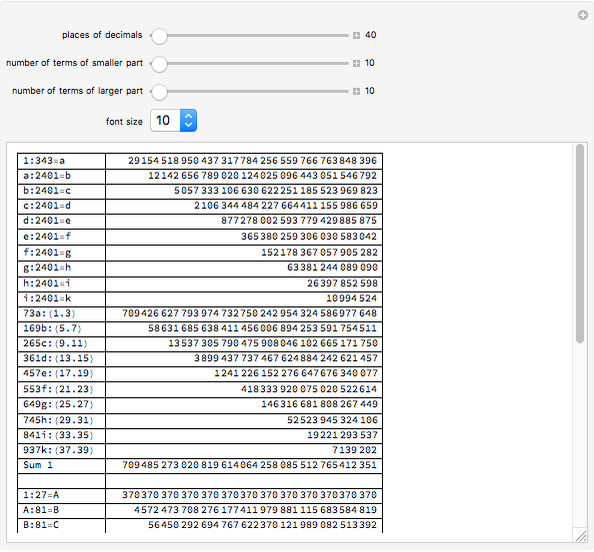
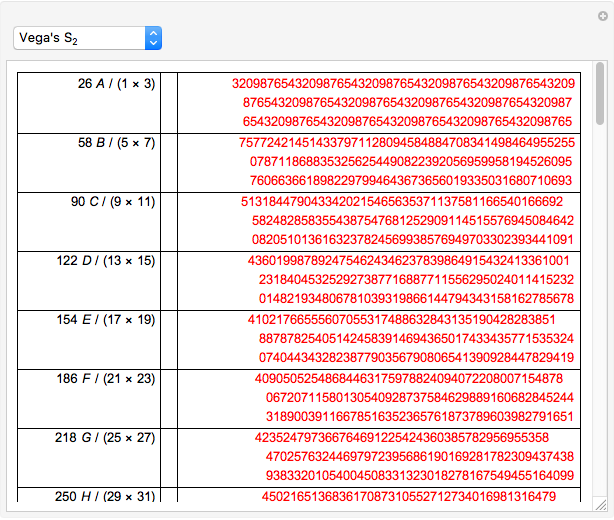
, which are simpler to calculate with. He illustrated this with the formula  . He calculated eight terms of the sum for each of the arc tangents on the right to 27 decimal places each and concluded that
. He calculated eight terms of the sum for each of the arc tangents on the right to 27 decimal places each and concluded that  . On the next page he calculated terms 9–16 of the first part and terms 9–10 of the second part and concluded that
. On the next page he calculated terms 9–16 of the first part and terms 9–10 of the second part and concluded that  . To eighteen places,
. To eighteen places,  . To 30 places,
. To 30 places,  .
.
Contributed by: Izidor Hafner (June 2013)
Open content licensed under CC BY-NC-SA
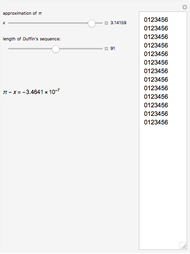
Snapshots
Details
See [2] for a history of Euler's attempts to calculate an approximation to  . The calculations from [1, p. 141] are added.
. The calculations from [1, p. 141] are added.
References
[1] L. Euler, "Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae," Nova Acta Academiae Scientarum Imperialis Petropolitinae 11, 1798, pp. 133-149. www.math.dartmouth.edu/~euler/tour/tour_08.html.
[2] E. Sandifer. "How Euler Did It: Estimating  ." MAA Online. Feb 2009. (Jun 20, 2013).
." MAA Online. Feb 2009. (Jun 20, 2013).
Permanent Citation