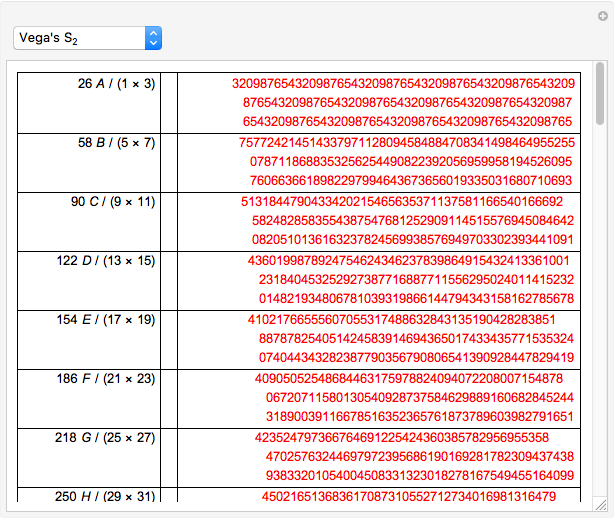
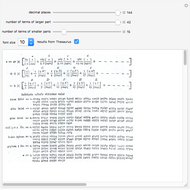
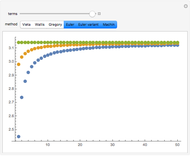
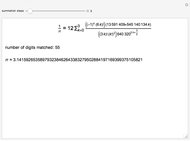
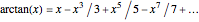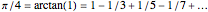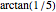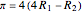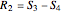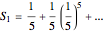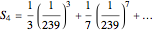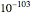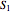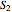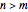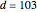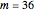Machin's Computation of Pi

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
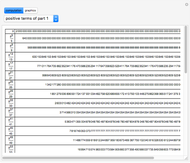
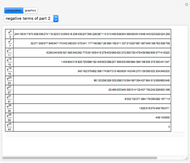
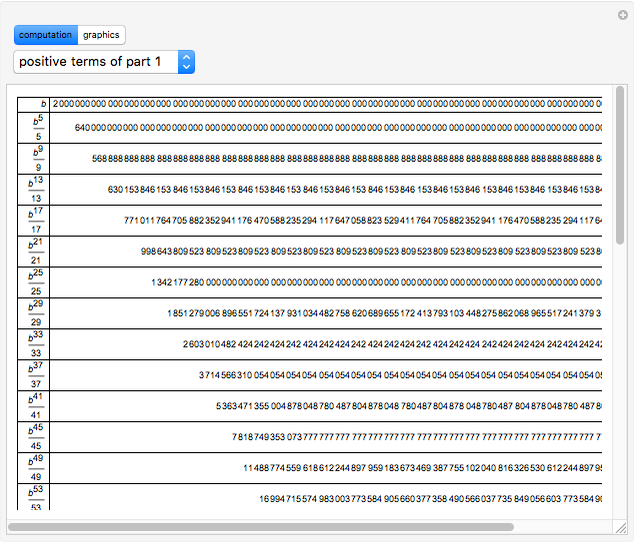
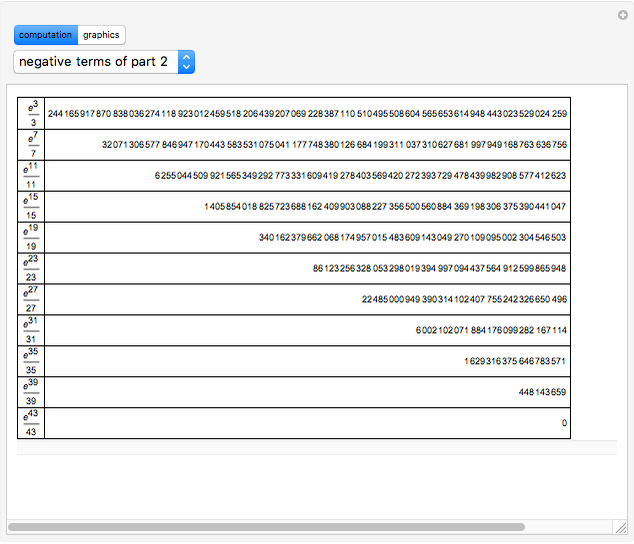
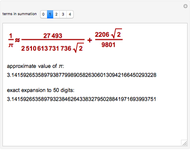
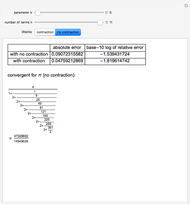
Around 1706, John Machin found the arc tangent formula 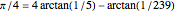 .
.
Contributed by: Izidor Hafner (May 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
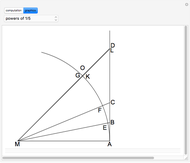
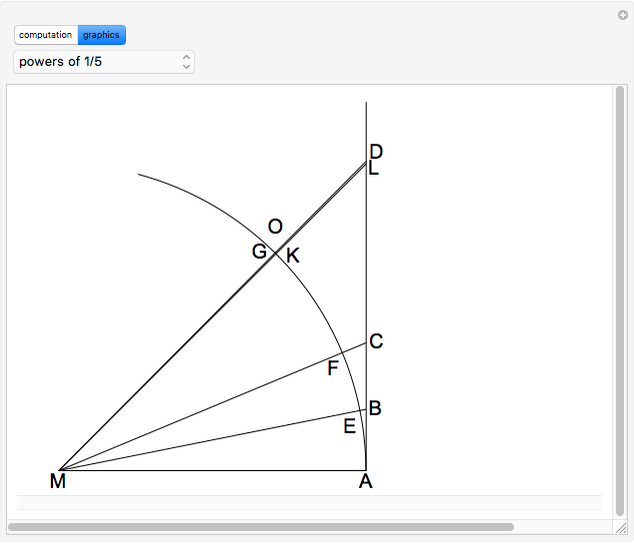
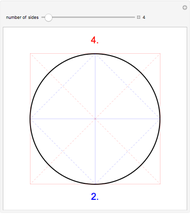
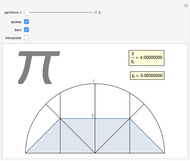
Let 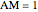 ,
, 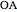 be an arc of radius 1, and
be an arc of radius 1, and  be perpendicular to
be perpendicular to 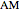 ,
,  ,
, 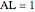 , and
, and 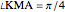 . Construct points
. Construct points 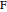 and
and  on the arc
on the arc  , and
, and  and
and  on the straight line
on the straight line 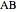 , so that
, so that 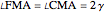 and
and  .
.
Then  and
and  ,
, 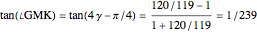 .
.
So 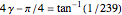 ,
, 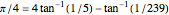 .
.
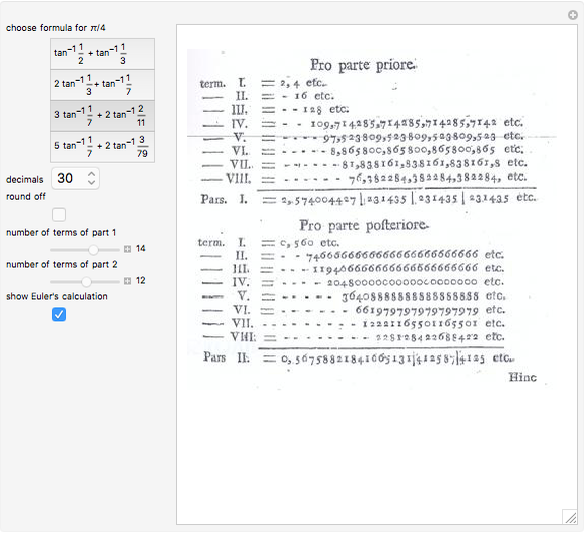
See [1, pp. 8–9].
References
[1] V. F. Rickey. "Machin's Formula for Computing Pi." (Apr 28, 2016) fredrickey.info/talks/10-03-13-HPM-DC-Machin/10-03-13-HPM_DC_Machin.pdf.
[2] MacTutor. "John Machin." (Apr 28, 2016) www-history.mcs.st-andrews.ac.uk/Biographies/Machin.html.
[3] Wikipedia. "John Machin." (Apr 28, 2016) en.wikipedia.org/wiki/John_Machin.
[4] W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, 13th ed., New York: Dover Publications, 1987 p. 356.
Permanent Citation