Wolfram Demonstrations Project

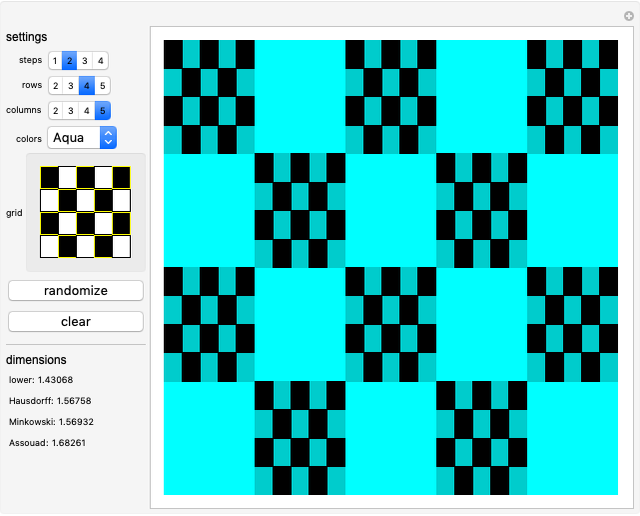
Bedford–McMullen carpets are planar fractals that generalize the Sierpinski carpet. In this Demonstration, you can plot all possible Bedford–McMullen carpets of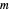

rows and

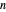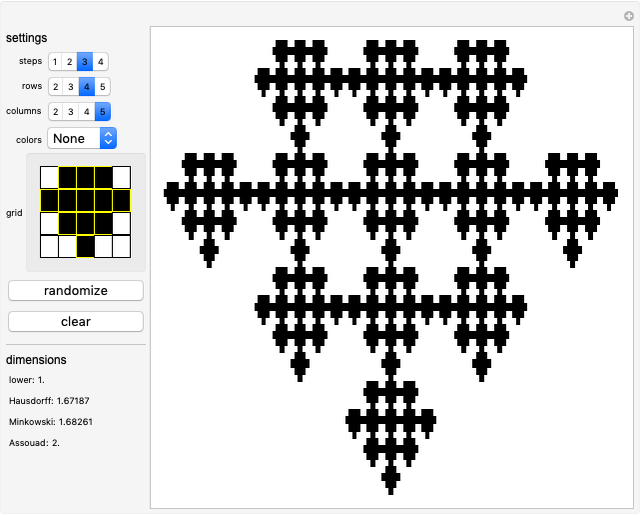
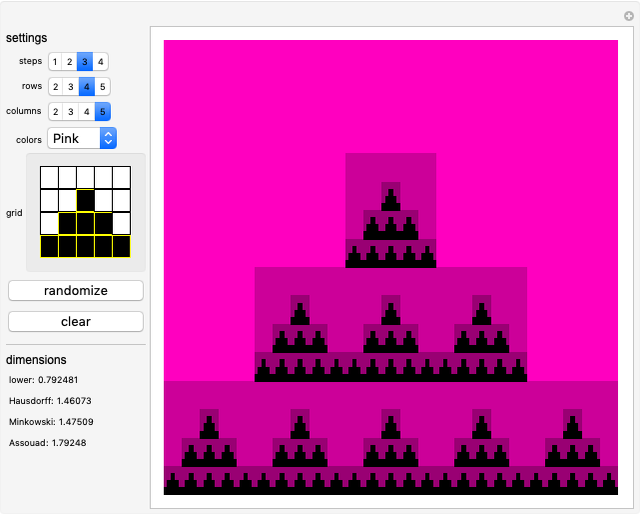
columns, with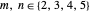

, up to step 4 of the construction. The display shows the lower, Hausdorff, Minkowski and Assouad dimensions of the plotted carpet.

Contributed by: Efstathios Konstantinos Chrontsios Garitsis, Xiaojun Jia and Troy Yang

Automatic Animation

The construction of a Bedford–McMullen carpet proceeds as follows:

1. Take the unit square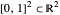

and pick two numbers

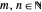2. Separate the unit square into an

grid of axes-oriented rectangles.

3. Select which rectangles to keep and erase the rest.

4. In each remaining rectangle, apply the same construction, that is, separate it into a grid and keep the same rectangles as before.

Continuing infinitely many times will result in a planar fractal.

A rigorous definition of what we described above is the following:

Definition: Let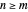

and a fixed, nonempty set

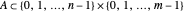. We call the self-affine set

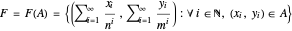
a Bedford-McMullen carpet of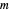

rows and

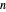columns.

The set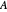

determines the rectangles that are kept during the construction, and, more specifically, it is the set of lower-left vertices of the rectangles that are kept with

coordinates multiplied by

and

coordinates multiplied by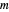

Moreover, our focus is on the case where

because many of the following formulas are easier to express. If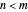

, we just apply a counterclockwise rotation by 90 degrees and a translation to the right by 1 to the unit square, and we return to the case where

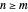without changing any of the dimensions of the carpet and the following formulae still hold.

Theorem: Let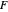

be a Bedford–McMullen carpet and denote by

the number of chosen rectangles to keep,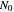

the number of columns containing at least one chosen rectangle and

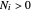the number of rectangles chosen in the

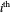nonempty column. Then the lower, Hausdorff, Minkowski and Assouad dimensions of

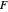are given by:

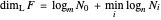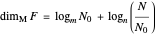and

The definitions of the given dimensions can be found in [1] and the proofs of the formulae can be found in [2–5]. Note that the code uses the same notation as that of MacKay in [5].

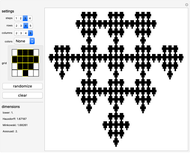
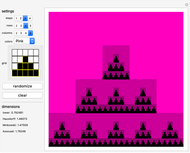
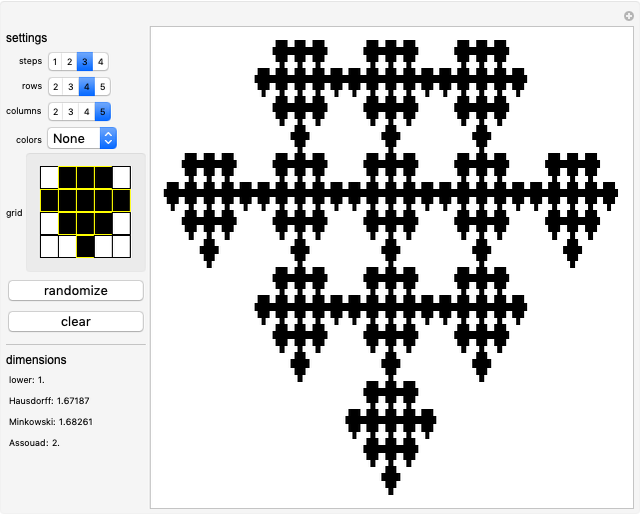
Using the given construction and formulae, this visualization offers a way to plot all possible Bedford–McMullen carpets of up to five rows and five columns. The plot depicts the fourth step of the construction, which is detailed enough and as close to the actual set as Mathematica can get (as of Version 12) since any step above 4 results in essentially the same image.

This Demonstration has options for:

 the number of steps in the construction,

 the number of rows for the carpet,

 the number of columns for the carpet,

 a choice of different colors for the background and the rectangles plotted in previous steps,

 an interactive grid where you can select the rectangles to keep (marked as black) or erase (marked as white),

 a "randomize" button to select rectangles to keep at random,

 a "clear" button to mark all rectangles white and

 a list of the dimensions of the carpet with the chosen settings.

For more theoretical background on dimensions and self-affine sets, see [1].

References

[1] J. M. Fraser, Assouad Dimension and Fractal Geometry, New York: Cambridge University Press, 2021.

[2] T. J. Bedford, "Crinkly Curves, Markov Partitions and Box Dimensions in Self-Similar Sets," Ph.D. thesis, University of Warwick, 1984. webcat.warwick.ac.uk/record=b1464305~S1.

[3] J. M. Fraser, "Assouad Type Dimensions and Homogeneity of Fractals," Transactions of the American Mathematical Society, 366(12), 2014 pp. 6687–6733. doi:10.1090/S0002-9947-2014-06202-8.

[4] C. T. McMullen, "Hausdorff Dimension of General Sierpinski Carpets," Nagoya Mathematical Journal, 96, 1984 pp. 1–9.

[5] J. M. MacKay, "Assouad Dimension of Self-Affine Carpets," Conformal Geometry and Dynamics, 15, 2011 pp. 177–187. doi:10.1090/S1088-4173-2011-00232-3.