Fractal Curves Generated by Fourier Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Given a sequence of coefficients 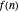 ,
, 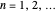 , write the Fourier series
, write the Fourier series 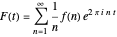 . For
. For 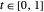 , the plot of
, the plot of 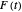 traces out a closed curve in the complex plane. This Demonstration shows this curve for some selected choices of the coefficients
traces out a closed curve in the complex plane. This Demonstration shows this curve for some selected choices of the coefficients 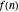 .
.
Contributed by: Nick Kokkines, Andre Park, Efstathios Konstantinos Chrontsios Garitsis and A. J. Hildebrand (August 2022)
(Based on an undergraduate research project at the Illinois Geometry Lab in Fall 2021)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is inspired by a 1995 paper by J. Bohman and C.-E. Fröberg [1] investigating the Fourier series
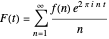
for various classes of oscillating coefficients 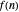 . In many cases, they observed remarkable fractal-like patterns in the plots of
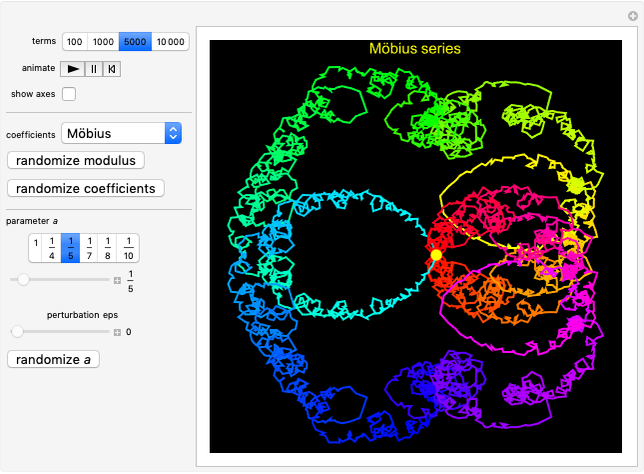
. In many cases, they observed remarkable fractal-like patterns in the plots of 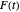 . More recent work by E. Kowalski and W. F. Sawin [2] examines the behavior of series of this type from a probabilistic point of view. Their work sheds some light on the peculiar shape of the curve traced out by
. More recent work by E. Kowalski and W. F. Sawin [2] examines the behavior of series of this type from a probabilistic point of view. Their work sheds some light on the peculiar shape of the curve traced out by 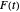 when the coefficients
when the coefficients 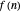 are given by the Möbius function.
are given by the Möbius function.
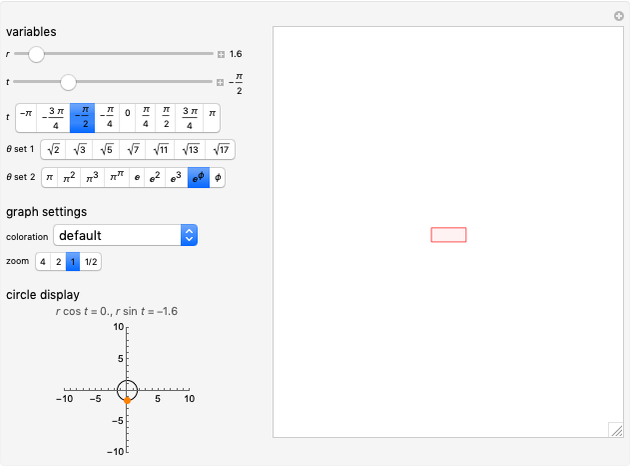
This Demonstration shows the closed curve in the complex plane traced out by 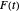 as
as  ranges from 0 to 1 for the following coefficient sequences
ranges from 0 to 1 for the following coefficient sequences 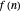 :
:
Möbius:  , where
, where  is the Möbius function.
is the Möbius function.
Jacobi symbol:  , where the modulus
, where the modulus 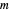 is a prime in the range
is a prime in the range  , selected randomly. Use the "randomize modulus" button to generate a new randomization.
, selected randomly. Use the "randomize modulus" button to generate a new randomization.
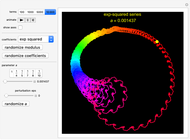
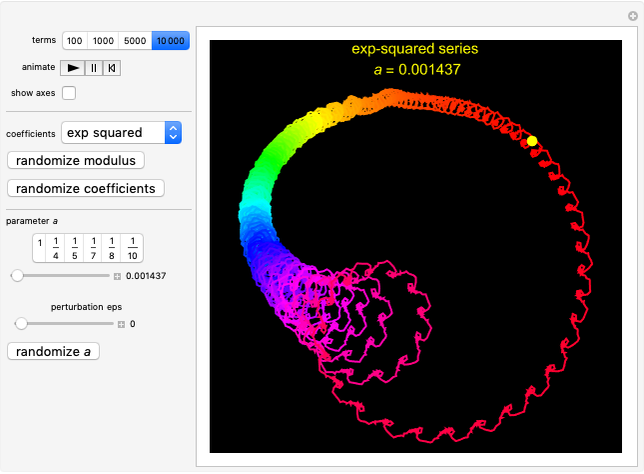
Exp-squared: 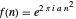 , in which you set the parameter
, in which you set the parameter 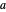 in the range
in the range  . Of particular interest is the behavior of the associated Fourier series
. Of particular interest is the behavior of the associated Fourier series  in the case when the parameter
in the case when the parameter 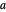 is close to a rational number with a small denominator. To study this behavior, this Demonstration offers a list of predefined rational values for
is close to a rational number with a small denominator. To study this behavior, this Demonstration offers a list of predefined rational values for 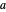 . Use the "perturbation" slider to perturb the parameter
. Use the "perturbation" slider to perturb the parameter 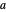 over a narrow range.
over a narrow range.
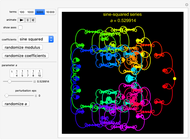
Sine-squared: 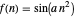 , for selected parameter
, for selected parameter 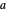 .
.
Fractional part:  , for selected parameter
, for selected parameter 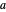 . The braces denote the fractional part.
. The braces denote the fractional part.
Tangent: 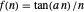 , for selected parameter
, for selected parameter 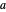 .
.
randomize coefficients: 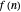 is selected randomly, with uniform probability, from
is selected randomly, with uniform probability, from 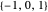 . Use the "randomize coefficients" button to generate a new randomization.
. Use the "randomize coefficients" button to generate a new randomization.
Implementation Notes
This Demonstration uses the built-in Mathematica function Fourier, which, given a list of  complex numbers, outputs the discrete Fourier transform of this list. Applying this function to the list
complex numbers, outputs the discrete Fourier transform of this list. Applying this function to the list 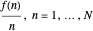 , we obtain an approximation to the Fourier series
, we obtain an approximation to the Fourier series 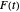 , sampled at
, sampled at 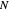 equally spaced points
equally spaced points  . The path shown in this Demonstration is the polygonal path through these
. The path shown in this Demonstration is the polygonal path through these  sampled points. Use the "terms" control to select the truncation value
sampled points. Use the "terms" control to select the truncation value 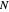 . Larger values provide a more accurate approximation to the true path of
. Larger values provide a more accurate approximation to the true path of 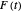 , while smaller values lead to smoother animations of these paths.
, while smaller values lead to smoother animations of these paths.
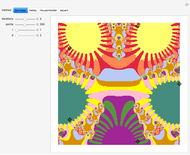
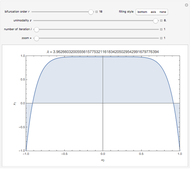
Snapshot 1: Exp-squared series, with 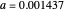 and
and 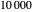 steps to show more detail. Changing the perturbation will vary the size, shape and position of the fractal-like patterns.
steps to show more detail. Changing the perturbation will vary the size, shape and position of the fractal-like patterns.
Snapshot 2: Sine-squared series, with 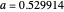 and
and 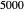 steps. Showing more steps will show more detail, and changing the perturbation will vary the size, shape and position of the fractal-like patterns.
steps. Showing more steps will show more detail, and changing the perturbation will vary the size, shape and position of the fractal-like patterns.
Snapshot 3: Tangent series, with 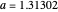 and
and  steps. Changing the perturbation will vary the size of the fractal-like patterns, from points to circles that almost fill the entire shape.
steps. Changing the perturbation will vary the size of the fractal-like patterns, from points to circles that almost fill the entire shape.
References
[1] J. Bohman and C.-E. Föberg, "Heuristic Investigation of Chaotic Mapping Producing Fractal Objects," BIT Numerical Mathematics, 35, 1995 pp. 609–615. doi:10.1007/BF01739831.
[2] E. Kowalski and W. F. Sawin, "Kloosterman Paths and the Shape of Exponential Sums," Compositio Mathematica, 152(7), 2016 pp. 1489–1516. doi:10.1112/S0010437X16007351.
Permanent Citation