Rep-tiles and Fractals of Order Five

Initializing live version

Rep-tiles and fractals of order five are defined as iterated function systems (IFS) and evaluated via the "chaos game" method.

Contributed by: Dieter Steemann (December 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

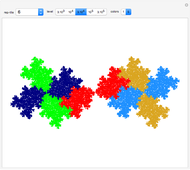
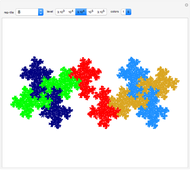
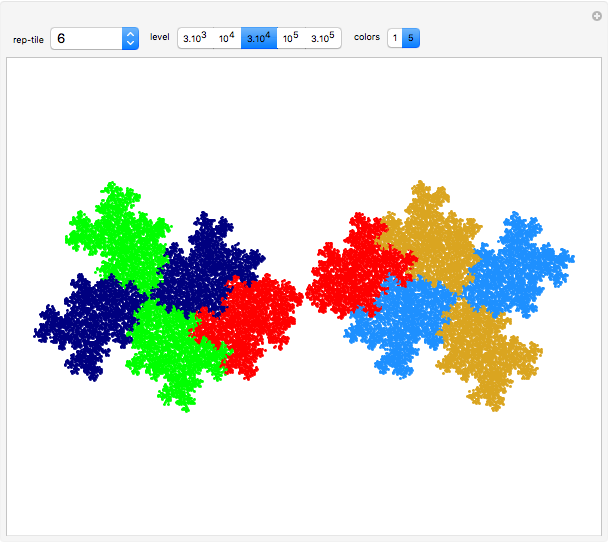
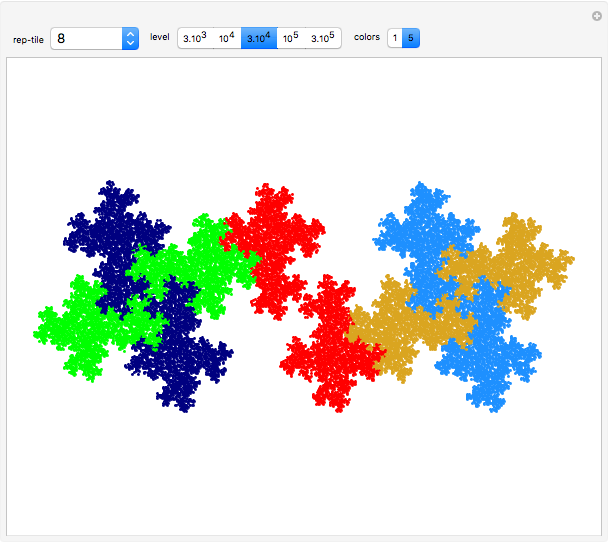
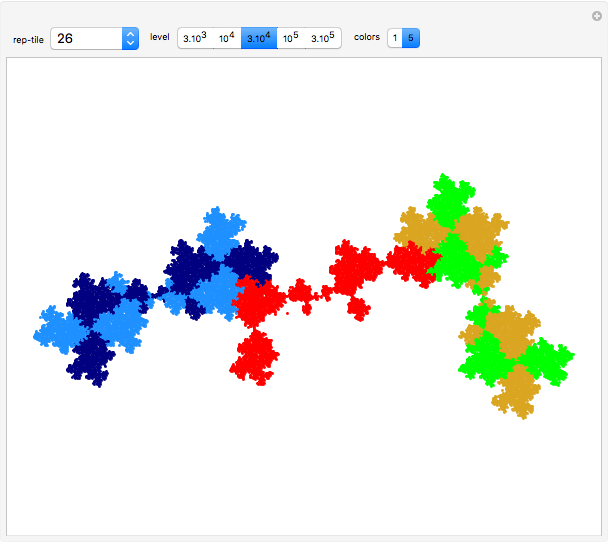
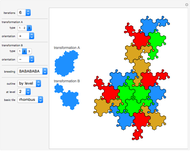
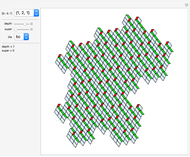
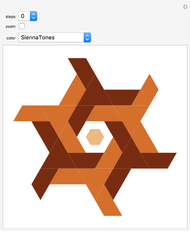
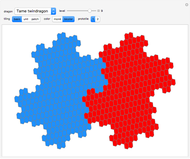
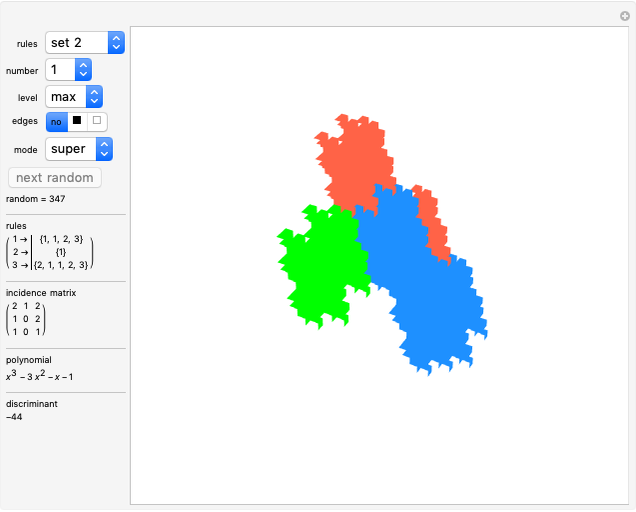
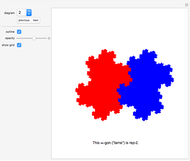
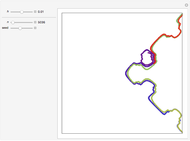
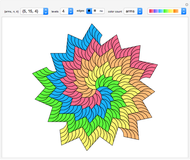
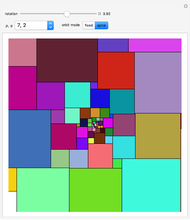
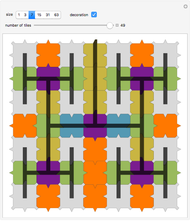
This Demonstration deals with the uncommon fractal rep-tiles of order five. Rep-tiles are plane figures that can be dissected into congruent smaller figures, possibly by a reflection. Fractal rep-tiles are also called frac-tiles. All shapes shown in this Demonstration can be combined into unit tiles that tile the plane periodically. The rep-tiles are defined as iterated function systems (IFS) and are evaluated via the "chaos game" method.

The rep-tile examples 1–4 follow the teardrop concept of Gosper [1]. Examples 5–8 and 23–38 are derived from these teardrops. A collection of space-filling curves that can be converted into tilings is given in [2]. All tilings in this Demonstration are based on a rotation angle 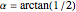that also appears in the well-known pinwheel tiling [3]. Hence, some of these show infinite orientations of subtiles, in which tiles are iteratively substituted by five smaller copies.

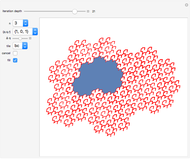
Only a few of the large variety of possible tile shapes are shown in examples 31–38. The miscellaneous examples 39–43 include the pinwheel tile and some irreptiles. Every rep-tile of order three can be converted into irreptiles of order five (see examples 41 and 42).

This collection is not complete. More rep-tiles and irreptiles of order five exist; see the Related Links.

Be patient when using the highest iteration level. In order to calculate 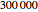image points, a lot of processing resources are required.

"Rep-tile" groups:

1–4 teardrop configuration: four tiles around a central point and a fifth tile like a teardrop at the outside

5–8 twin versions of examples in 1–4 (twofold rotational symmetry)

9–22 rep-tiles based on a triangular grid (11 is Mandelbrot's quartet)

23–30 half twins: two copies of these patterns combine into twins of examples in 5–8

31–34 quarter crosses: four copies of these patterns combine into a fractal cross

35–38 unconnected patterns: two copies combined into twins of examples in 5–8

39–43 miscellaneous examples

References

[1] R. W. Gosper. "Teardrop Frac-n-tiles." (Dec 19, 2016) www.tweedledum.com/rwg/frac5.htm.

[2] J. Ventrella, "The Root 5 Family, a Chapter from Brainfilling Curves." (Dec 19, 2016) www.fractalcurves.com/Root5.html.

[3] Wikipedia. "Pinwheel Tiling." (Dec 19, 2016) en.wikipedia.org/wiki/Pinwheel_tiling.

Permanent Citation

Dieter Steemann "Rep-tiles and Fractals of Order Five"
http://demonstrations.wolfram.com/RepTilesAndFractalsOfOrderFive/
Wolfram Demonstrations Project
Published: December 21 2016


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send