Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bicycle Rides

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

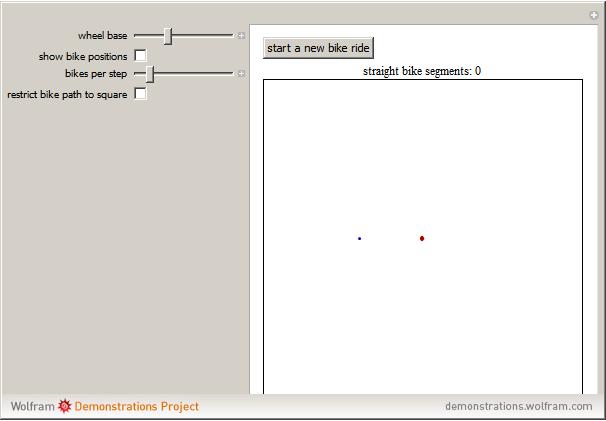
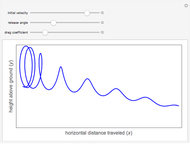
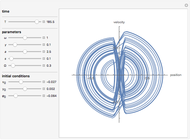
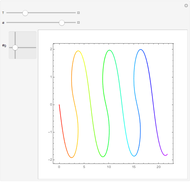
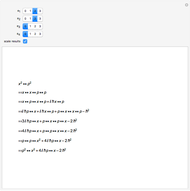
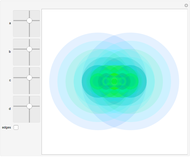
Hundreds of millions of people ride bicycles every day. Yet only a small fraction are aware of the multitude of beautiful mathematics and physics involved. Describing a bicycle ride requires the mechanics of nonholonomic multi‐body systems, control theory, and algebraic geometry.

[more]

Drag the front wheel (red point) of an idealized bicycle in the plane. Given its path, the path of the rear wheel is uniquely determined (through a set of coupled nonlinear differential equations). Depending on the length of the wheel base and the curvature of the path of the front wheel, the path of the rear wheel exhibits characteristic cusps.

[less]

Contributed by: Michael Trott with permission of Springer (March 2011)
From: The Mathematica GuideBook for Numerics, second edition by Michael Trott (© Springer, 2008).
Open content licensed under CC BY-NC-SA

Snapshots

Details

For modeling bicycle rides in general, see:

D. J. N. Limebeer and R. S. Sharp, "Bicycles, Motorcycles and Models," IEEE Control Systems Magazine, 26(5), 2006 pp.34–61.

S. R. Dunbar, R. J. C. Bosman and S. E. M. Nooij, "The Track of a Bicycle Back Tire," Mathematics Magazine, 74(4), 2001 pp.273–287.

M. Levi and S. Tabachnikov. "On Bicycle Tire Tracks Geometry, Hatchet Planimeter, Menzin's Conjecture and Oscillation of Unicycle Tracks." (Feb 3, 2008) http://arxiv.org/pdf/0801.4396.

Permanent Citation

Michael Trott with permission of Springer "Bicycle Rides"
http://demonstrations.wolfram.com/BicycleRides/
Wolfram Demonstrations Project
Published: March 7 2011

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send