Multiple Reflections of a Superball

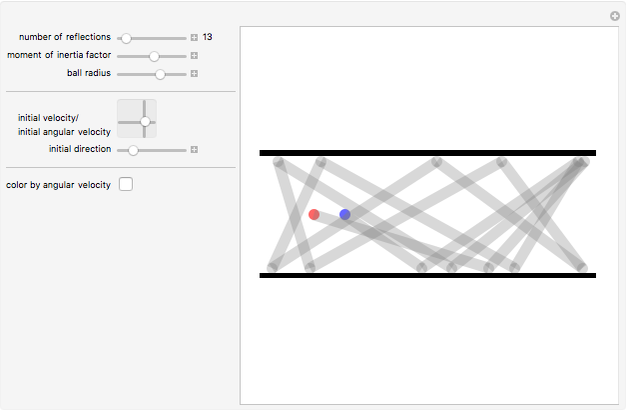
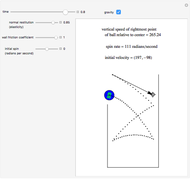
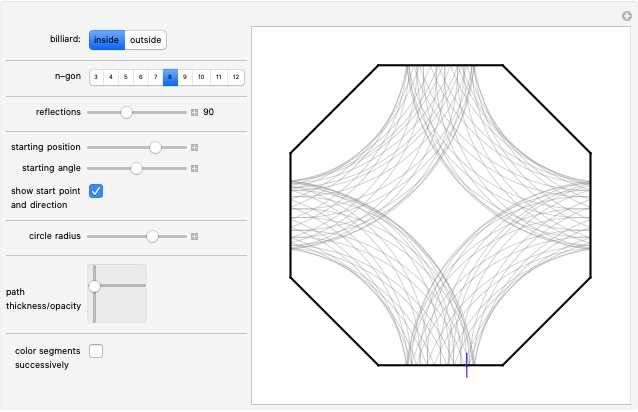
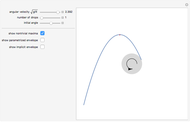
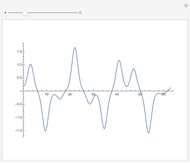
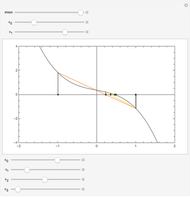
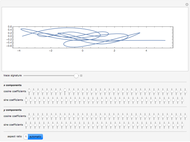
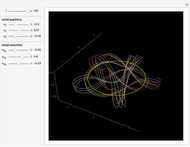
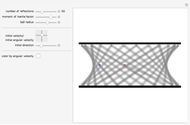
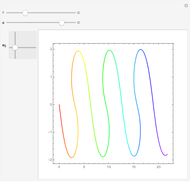
This Demonstration shows the path of a multiply reflected superball in a horizontal channel (ignoring gravity). At each reflection, the energy and the angular momentum of the ball are conserved, but due to friction, translational and rotational energy can be converted into each other. The initial position of the ball is the red point and the final position is the blue point

The graphic is scaled so that all reflections are shown and angles are not distorted.