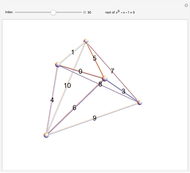
Five points in 4-space with no four on a plane make a 4D simplex (or hypertetrahedron)  . A Cayley–Menger determinant uses the 10 edge lengths of
. A Cayley–Menger determinant uses the 10 edge lengths of  to find the hypervolume.
to find the hypervolume.
Five points are called flat if the hypervolume of  is zero. This is also called a 3D degenerate simplex.
is zero. This is also called a 3D degenerate simplex.
Four points are called plane if the bounding volume of  is zero. This is also called a 2D degenerate tetrahedron.
is zero. This is also called a 2D degenerate tetrahedron.
Three points are called straight if the bounding area of  is zero. This is also called a 1D degenerate triangle.
is zero. This is also called a 1D degenerate triangle.
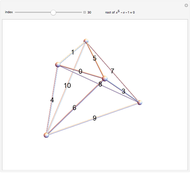
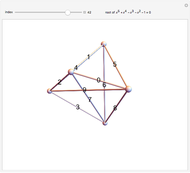
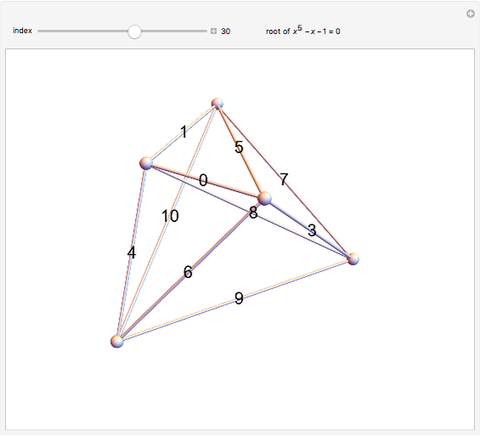
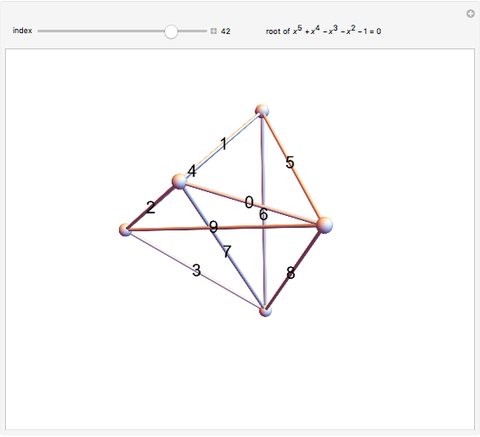
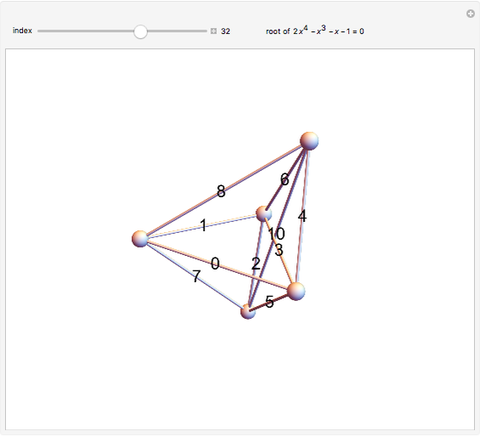
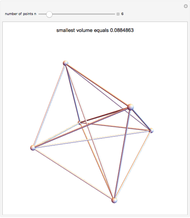
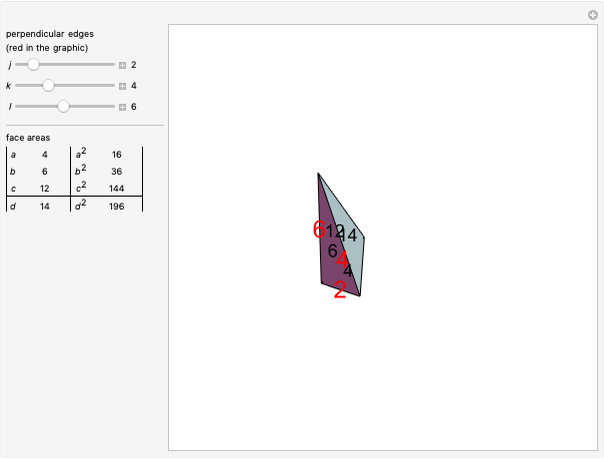
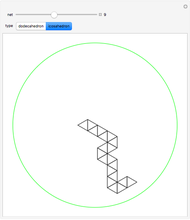
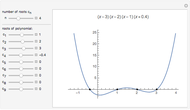
This Demonstration shows 50 3D degenerate simplices with the property that all the edge lengths are powers of a particular root. Each edge is labeled with the corresponding power. The edge 0 corresponds to length  and is always the shortest length.
and is always the shortest length.
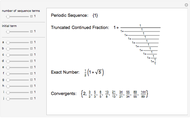
The plastic constant works very well (14 known solutions); it is a root of  (
( ), the smallest of the Pisot numbers. The next root that works well (10 known solutions) is a reciprocal of a root of
), the smallest of the Pisot numbers. The next root that works well (10 known solutions) is a reciprocal of a root of  (
( ), the next smallest Pisot number. So far, I have found 15 different algebraic roots of degree six or less that can make a 3D power simplex.
), the next smallest Pisot number. So far, I have found 15 different algebraic roots of degree six or less that can make a 3D power simplex.
The distances are actually powers of the square root of the given root. Index 51 has a degenerate tetrahedron, but I included it because it corresponds to the Narayana Cow constant, another of the Pisot numbers.
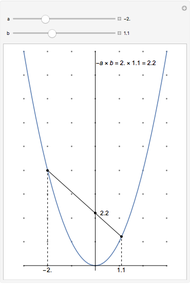
A degenerate 2D example uses root  , the golden ratio. The distances (0, 1, 2, 2, 1, 0) are powers of
, the golden ratio. The distances (0, 1, 2, 2, 1, 0) are powers of  , giving the
, giving the  rectangle with diagonals of length
rectangle with diagonals of length  . Removing a point gives the Kepler triangle.
. Removing a point gives the Kepler triangle.
What other solutions are there where the root has degree six or less? This Demonstration is meant as a starting point for this exploration.
[less]

 . A Cayley–Menger determinant uses the 10 edge lengths of
. A Cayley–Menger determinant uses the 10 edge lengths of  to find the hypervolume.
to find the hypervolume.