Seven Touching Cylinders Puzzle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
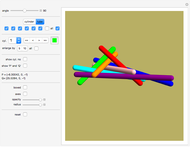
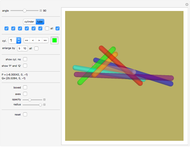
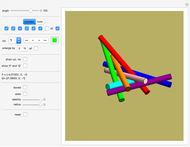
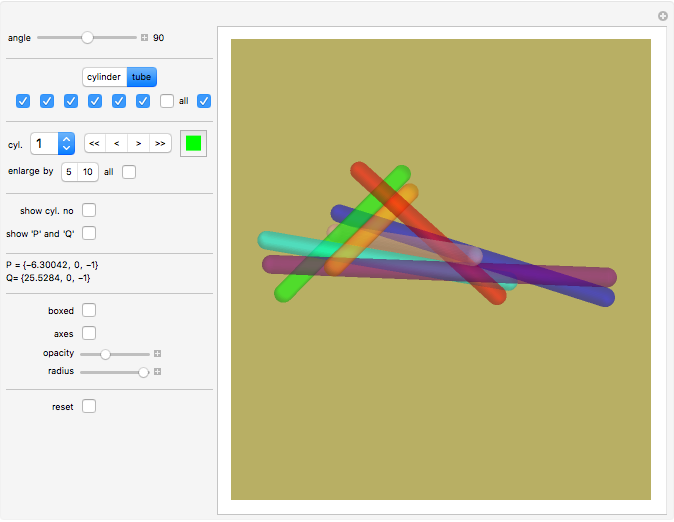
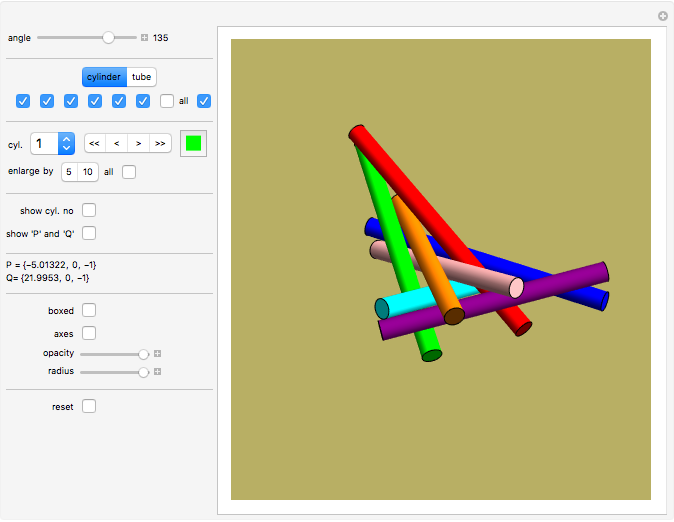
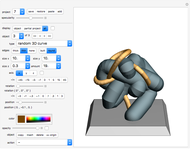
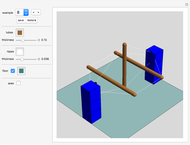
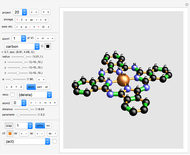
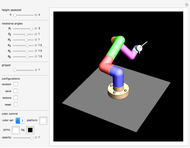
It was proven in May 2014 that seven cylinders of same radius can pairwise touch each other (not using the ends of the cylinders) without overlapping.
[more]
Contributed by: Karl Scherer (October 2014)
With additional contributions by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA
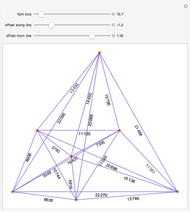
Snapshots
Details
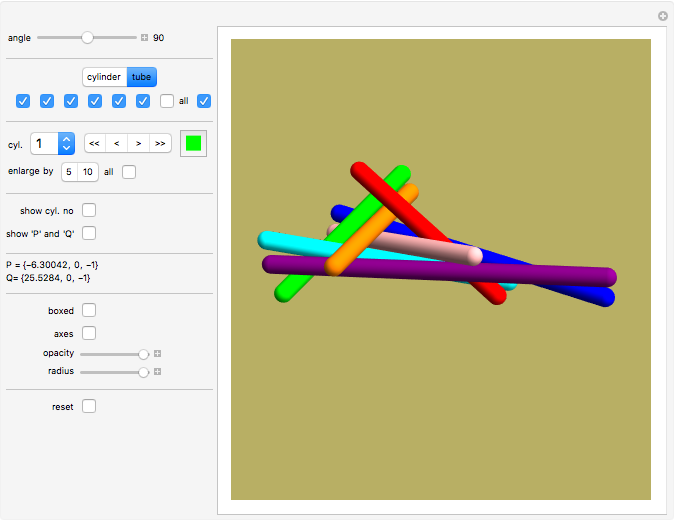
Controls
Move the "angle" slider to see the range of solutions.
The angle parameter is the angle between cylinder number 1 (blue) and cylinder number 2 (orange).
Select "cylinder" or "tube". Tubes have rounded ends only as an display option; the 7-cylinder-puzzle assumes that the cylinders have infinite length.
In the next line you have seven toggles which control which cylinder is being displayed. Click the "all" toggle to show them all.
Pop-up menu "cyl" (for "cylinder") lets you inspect each cylinder in details.
You can change the color of the current cylinder, for example, by clicking the swatch at the end of the row.
You can also elongate the current or all cylinders (in steps of 5 or 10 units, at both ends).
"show cyl no" displays the cylinder numbers.
"show P,Q" marks two points ("beginning" and "end") at the center of the displayed cylinder.
Below this the actual coordinates of P and Q are displayed.
Finally, we have a few controls which hardly need an explanation: zoom, boxed (shows 3D wire frame), axes, opacity, radius and reset button.
Contributions
Ed Pegg supplied the coordinates of the two points P and Q of each cylinder.
History
In May 2014 it was mathematically proven that seven non-overlapping cylinders of infinite length and same radius can touch each other (http://www.sciencedirect.com/science/article/pii/S0925772114000819). Two solutions have been found. A few months later a whole range of solutions was found.
Permanent Citation
"Seven Touching Cylinders Puzzle"
http://demonstrations.wolfram.com/SevenTouchingCylindersPuzzle/
Wolfram Demonstrations Project
Published: October 15 2014