Brownian Motion in 2D and the Fokker-Planck Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
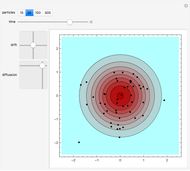
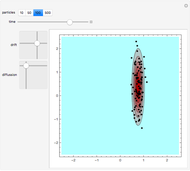
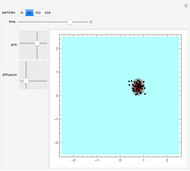
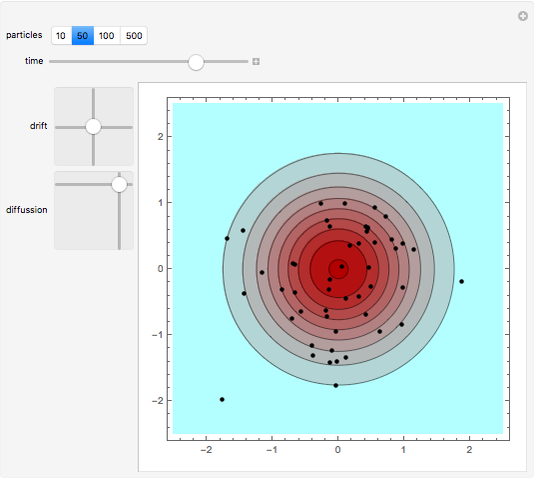
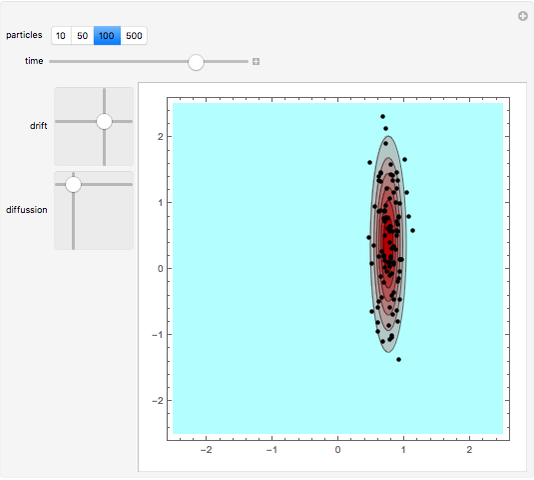
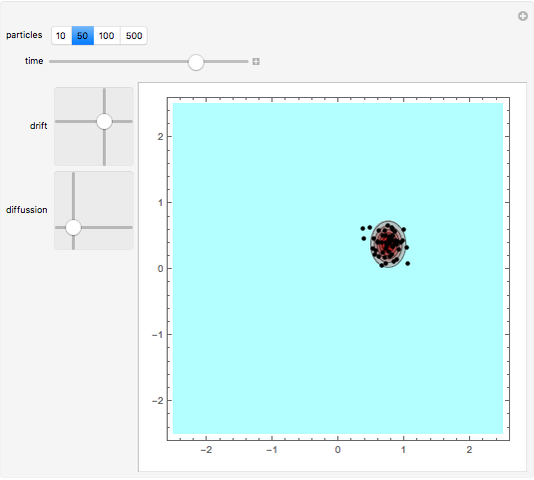
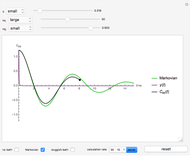
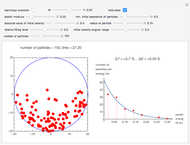
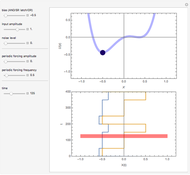
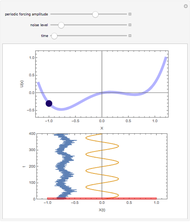
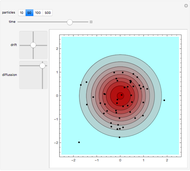
We show the Brownian motion of an evolving assembly of particles and the corresponding probability density. The probability density is a solution of the Fokker–Planck equation, which here reduces to a drift-diffusion partial differential equation. The center of mass of the particle distribution moves with a constant drift velocity while anisotropic diffusion is determined by the principal values of the diffusion matrix, along the Cartesian axes.
Contributed by: Alejandro Luque Estepa (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Brownian motion of a particle is described by a stochastic differential equation  , where the
, where the  are particle positions in
are particle positions in  ,
,  is the drift velocity,
is the drift velocity,  is an
is an  matrix and
matrix and  represents an
represents an  -dimensional normal Wiener process. The Fokker–Planck equation (also called forward Kolmogorov equation) describes the temporal evolution of the probability density
-dimensional normal Wiener process. The Fokker–Planck equation (also called forward Kolmogorov equation) describes the temporal evolution of the probability density  :
:
 , where
, where  .
.
If  and
and  are constant, the Fokker–Planck equation reduces to a drift-diffusion equation that can be solved analytically. The fundamental solutions are Gaussian distributions which drift and widen with time.
are constant, the Fokker–Planck equation reduces to a drift-diffusion equation that can be solved analytically. The fundamental solutions are Gaussian distributions which drift and widen with time.
This Demonstration shows the Brownian motion of a number of independent particles in 2D superimposed on the solution of the Fokker–Planck equation. To simplify the controls, the principal axes of the matrix  are always the horizontal-vertical axes of the screen.
are always the horizontal-vertical axes of the screen.
Permanent Citation