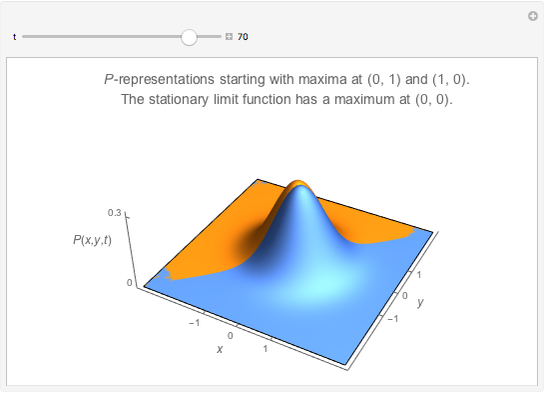
Shape-Invariant Solutions of the Quantum Fokker-Planck Equation for an Optical Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
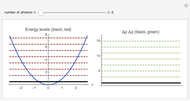
In quantum optics an equation of motion for the density operator  of an optical harmonic oscillator damped by a thermal bath of oscillators (reservoir) is derived. The optical mode may be described by the complex amplitude
of an optical harmonic oscillator damped by a thermal bath of oscillators (reservoir) is derived. The optical mode may be described by the complex amplitude  . The time-dependent Hermitian operator
. The time-dependent Hermitian operator  can be represented by a real-valued function
can be represented by a real-valued function 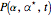 of the form
of the form  , the so-called
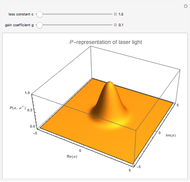
, the so-called  -representation. The equation of motion for
-representation. The equation of motion for 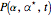 is the Fokker–Planck equation (FPE)
is the Fokker–Planck equation (FPE)  , where
, where  is the decay constant of the optical mode and
is the decay constant of the optical mode and  denotes the mean number of quanta in the thermal reservoir.
denotes the mean number of quanta in the thermal reservoir.
Contributed by: Reinhard Tiebel (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
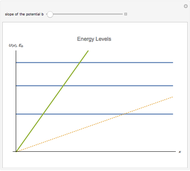
In their original meaning, the Fokker–Planck equations are partial differential equations for conditional probabilities in the theory of Markov processes, a special class of stochastic processes. In the quantum theory of a damped optical oscillator, Markovian properties also lead to a quantum FPE, valid for the quasi-probability density  .
.
The above functions were found as follows.
In the real variables  ,
,  , the FPE has the form
, the FPE has the form
 . The reduction to a one-dimensional equation of motion gives a simplified FPE, more complicated than the heat conduction equation:
. The reduction to a one-dimensional equation of motion gives a simplified FPE, more complicated than the heat conduction equation:
 . From the method of separation of variables in
. From the method of separation of variables in  and
and  , the formal solution is (special case:
, the formal solution is (special case:  ):
):
 , where
, where  are Hermite polynomials of order
are Hermite polynomials of order  . The coefficients
. The coefficients 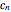 follow from the initial condition
follow from the initial condition  :
:  . The problem is that to obtain an analytical solution for
. The problem is that to obtain an analytical solution for  , either the integration or the summation cannot be carried out for many known elementary initial functions
, either the integration or the summation cannot be carried out for many known elementary initial functions  . In the case chosen here, when that the initial condition is the normalized function
. In the case chosen here, when that the initial condition is the normalized function  , then both operations (integration and summation) are possible; the result is
, then both operations (integration and summation) are possible; the result is
 . Returning to the original two-dimensional problem is easy:
. Returning to the original two-dimensional problem is easy:
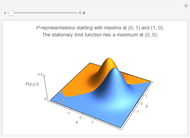
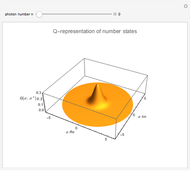
 is one of three quasi-probability densities normalized for all
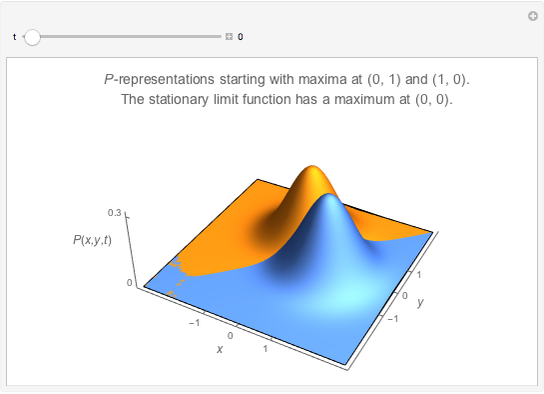
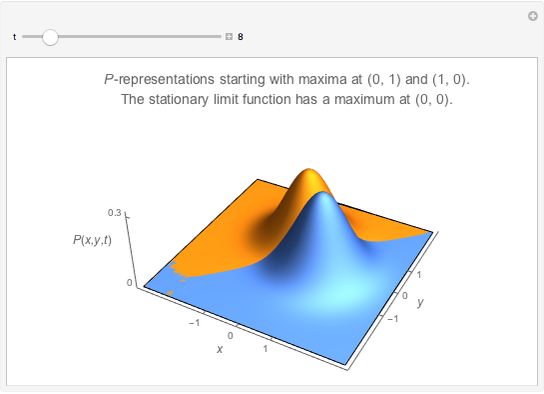
is one of three quasi-probability densities normalized for all  (this Demonstration shows two of three calculated functions).
(this Demonstration shows two of three calculated functions).
References
[1] M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge: Cambridge University Press, 1997.
[2] P. Meystre and M. Sargent III, Elements of Quantum Optics, Berlin Heidelberg: Springer Verlag, 1991.
[3] J. Perina, Coherence of Light, Dordrecht-Boston-Lancaster: D. Reidel Publishing Company, 1985.
[4] M. Abramowitz and I. A. Stegun, Pocketbook of Mathematical Functions, Frankfurt: Verlag Harri Deutsch, 1984.
[5] W. I. Smirnow, Lehrgang der Höheren Mathematik, Teil 2: Frankfurt: Verlag Harri Deutsch, 2004.
[6] W. S. Wladimirow, Gleichungen der mathematischen Physik, Berlin: Deutscher Verlag der Wissenschaften, 1972.
Permanent Citation