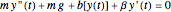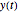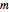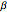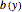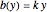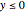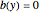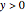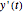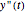Bungee Jumping
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
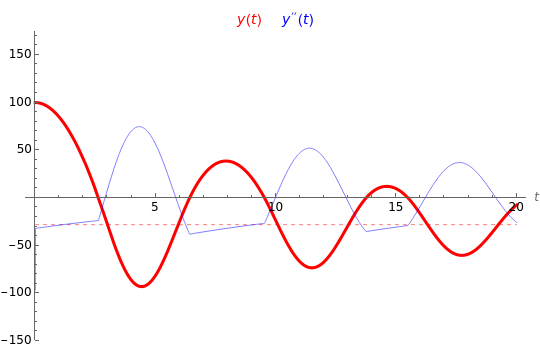
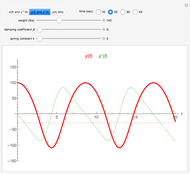
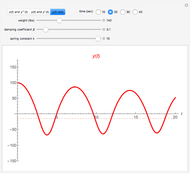
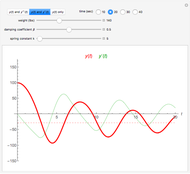
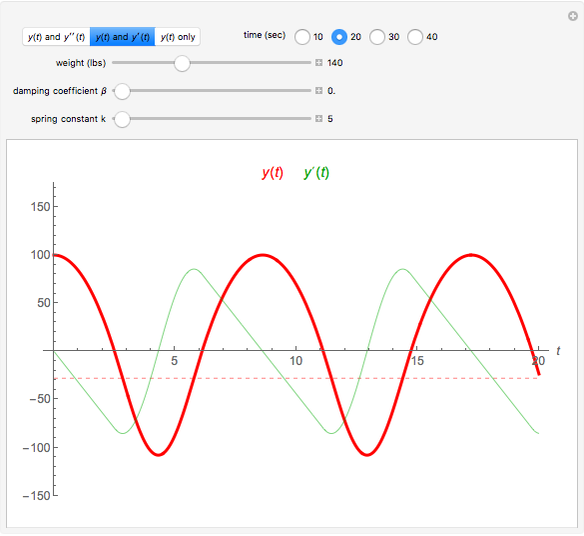
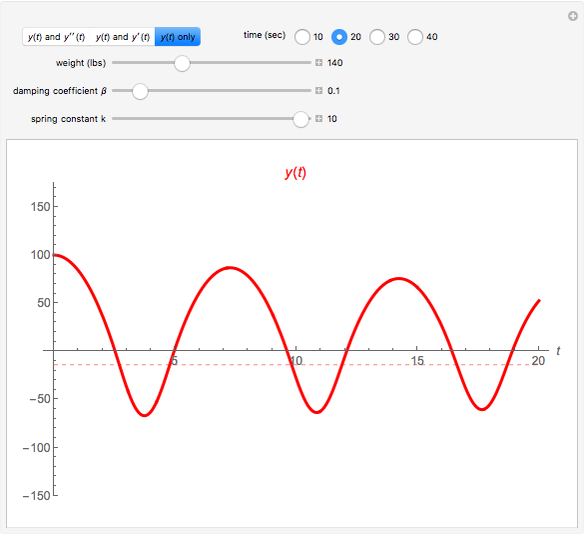
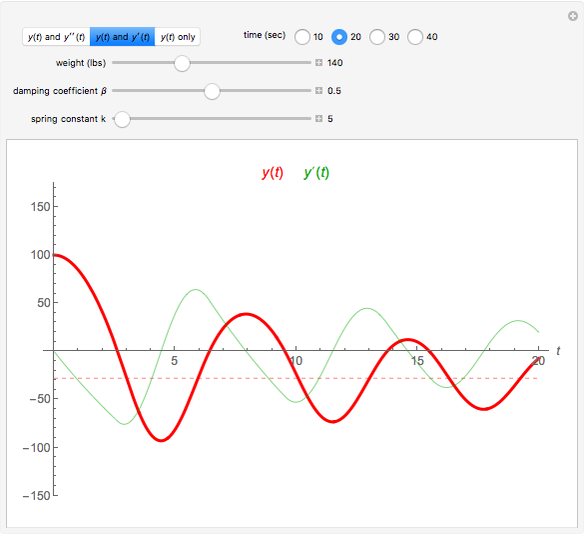
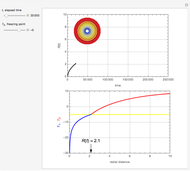
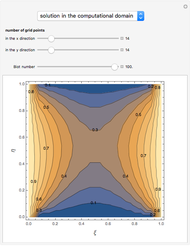
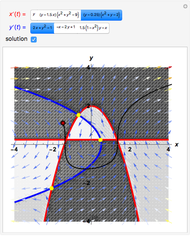
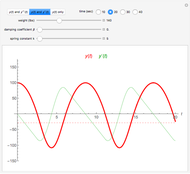
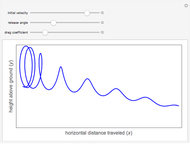
The following second-order nonlinear differential equation models a bungee jump:
[more]
Contributed by: Helmut Knaust (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation