Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Kiesswetter's Function

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

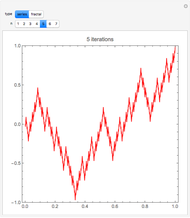
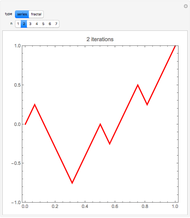
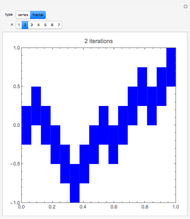
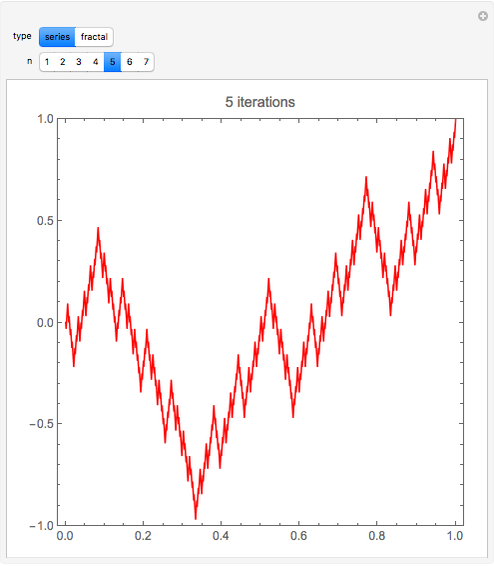
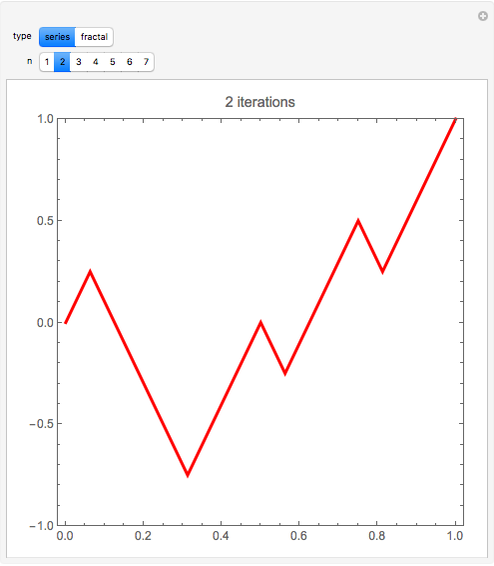
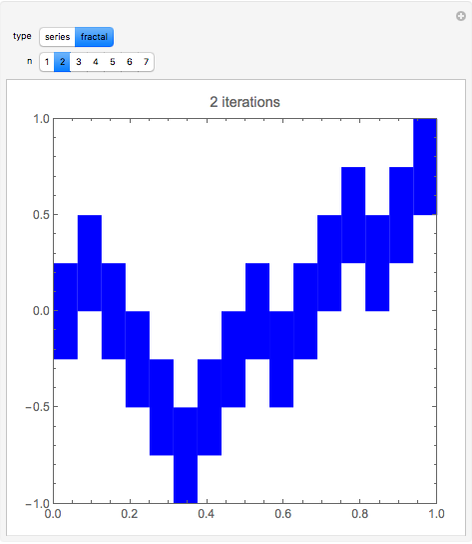
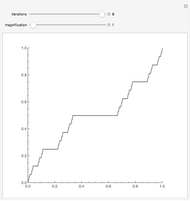
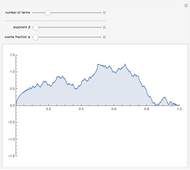
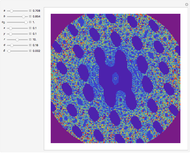
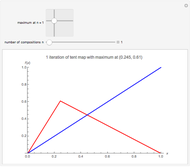
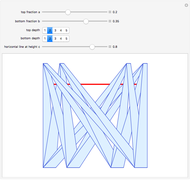
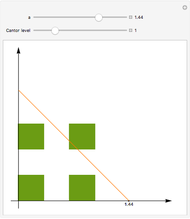
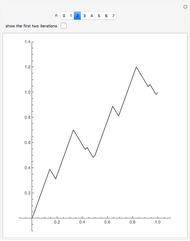
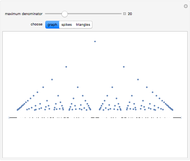
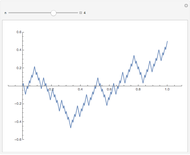
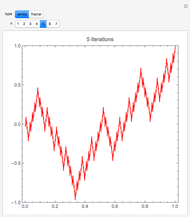
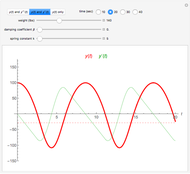
In 1966 Karl Kießwetter [1] introduced a simple example of a continuous nowhere differentiable function. He claims that the example can be understood by talented high school seniors.

[more]

We illustrate Kießwetter's function in two different ways: (1) as a limit of partial sums ("series"), and (2) as an intersection of sets ("fractal"). The second definition is due to Gerald A. Edgar [2].

[less]

Contributed by: Helmut Knaust (June 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The first example of a continuous nowhere differentiable function was found by Karl Weierstraß in 1872.

More examples were found by Bernard Bolzano, Charles Cellérier, Bartel L. van der Waerden, Teiji Tagaki, Theophil H. Hildebrandt, and others.

References

[1] K. Kiesswetter, "Ein einfaches Beispiel für eine Funktion, welche überall stetig und nicht differenzierbar ist," Mathematisch-Physikalische Semesterberichte, 13, 1966 pp. 216–221.

[2] G. A. Edgar, Measure, Topology, and Fractal Geometry, New York: Springer-Verlag, 1990.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send