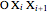Calculating the Area of a Country Using Green's Theorem
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Green's theorem shows the relationship between the length of a closed path and the area it encloses.
[more]
Contributed by: Erik Mahieu (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
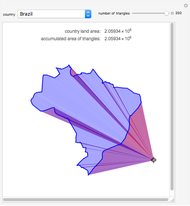
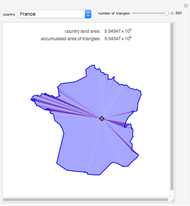
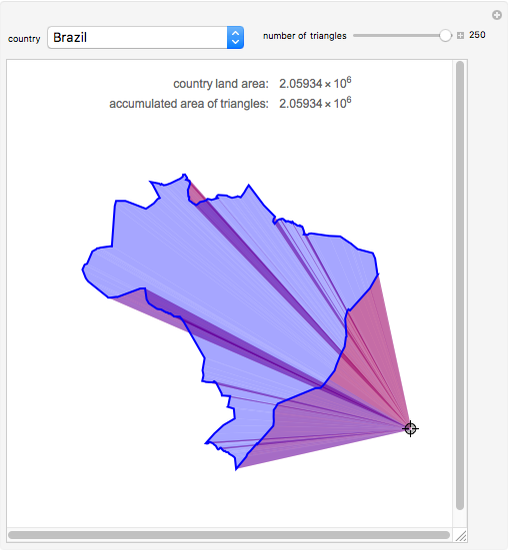
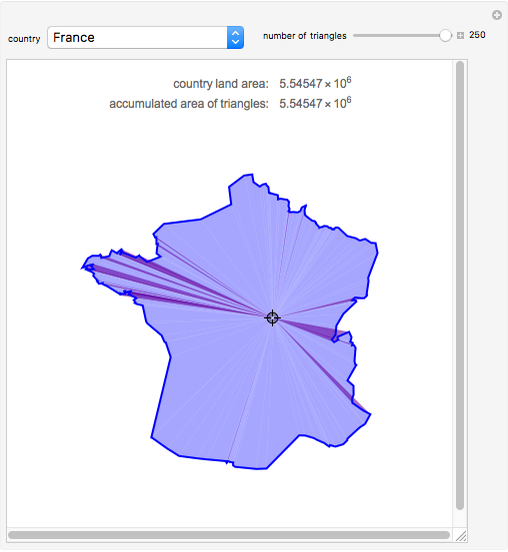
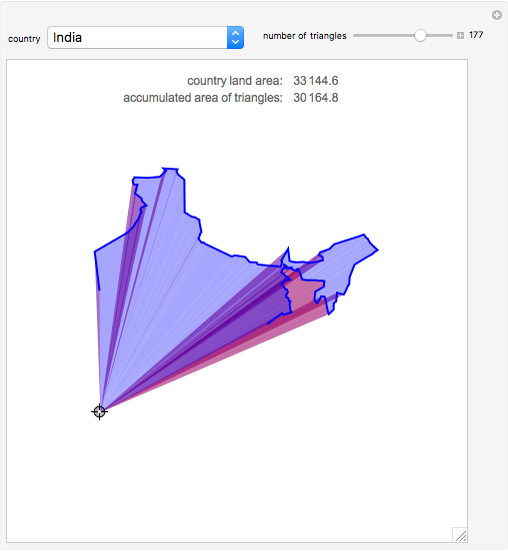
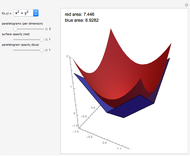
Snapshot 1: Shows the total area being independent of the position of the locator.
Snapshot 2: Shows the mostly positive areas (determinants) if the locator is in the middle. The direction of Mathematica's CountryData coordinates is clockwise.
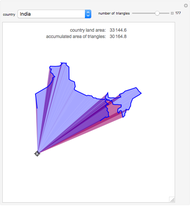
Snapshot 3: This illustrates the red positive areas and the blue negative ones. An intermediate color is generated when they overlap.
Permanent Citation