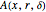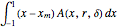Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Center of Mass of Disk with Circular Hole

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

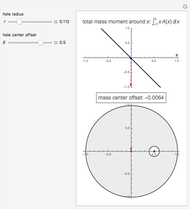
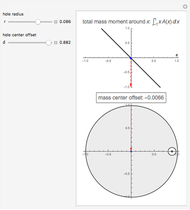
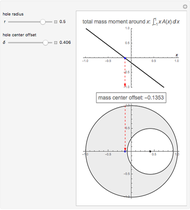
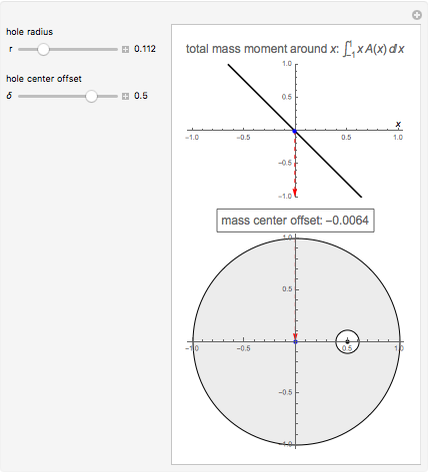
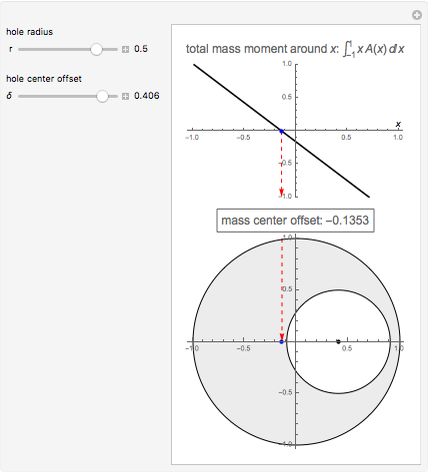
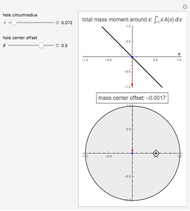
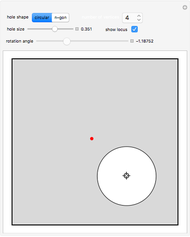
This Demonstration computes the center of mass of a disk 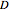of radius 1 with a circular hole of radius located at a distance from the center of .

[more]

The surface area function integrates the difference between the circular edge of the disk and that of the hole up to some position on the axis.

The abscissa of the center of mass is computed as the value for which the integral is equal to zero.

[less]

Contributed by: Erik Mahieu (April 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Since the disk and the hole are symmetrical with respect to the axis, the coordinate of the center of mass of the upper half is the coordinate of the center of mass of the entire disk and hole. Therefore, only the upper half needs to be considered.

The function

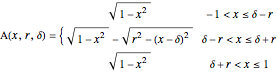
defines the difference between the disk's outer circle and the edge of the circular hole. This is the net surface area at .

The function is the total mass moment relative to .

Solving the equation for 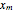gives the abscissa of the center of mass.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send