Chromatic Spindles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
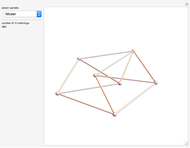
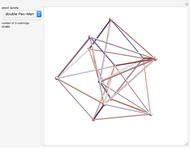
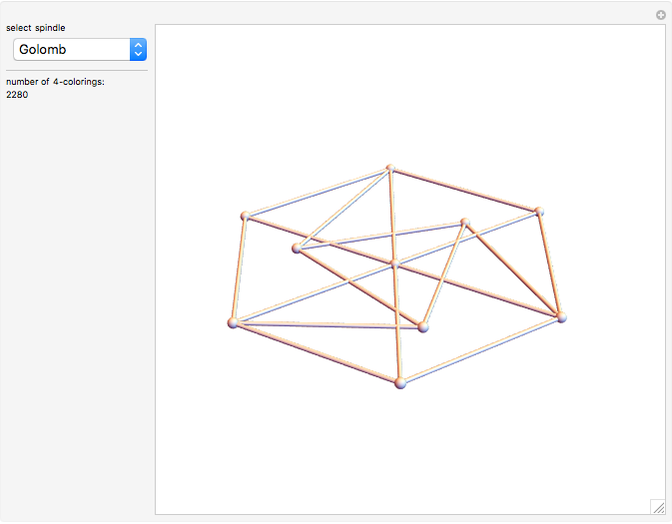
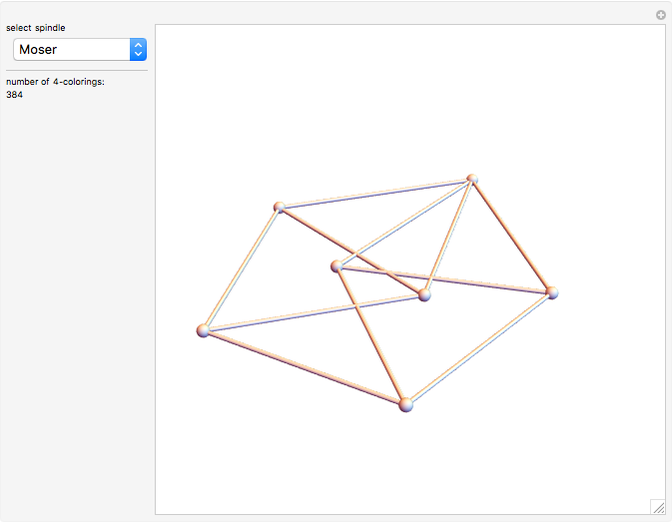
Color the plane so that no two points of the same color are at distance 1 apart. How many colors are needed? If instead, 3D space is colored, how many colors are needed there? Both are unsolved problems! The chromatic number of the plane is 4, 5, 6, or 7. This question is known as the Hadwiger–Nelson problem. In space, the range of possible values is 6–15.
[more]
Contributed by: Ed Pegg Jr (October 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] Wikipedia. "Hadwiger–Nelson Problem." (Oct 22, 2015) en.wikipedia.org/wiki/Hadwiger% E2 %80 %93 Nelson_problem.
[2] D. Coulson, "A 15-Colouring of 3-Space Omitting Distance One," Discrete Mathematics, 256(1–2), 2002 pp. 83–90. doi:10.1016/S0012-365X(01)00183-2.
[3] O. Nechushtan, "On the Space Chromatic Number," Discrete Mathematics, 256(1–2), 2002 pp. 499–507. doi:10.1016/S0012-365X(00)00406-4.
Permanent Citation
"Chromatic Spindles"
http://demonstrations.wolfram.com/ChromaticSpindles/
Wolfram Demonstrations Project
Published: October 26 2015