Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

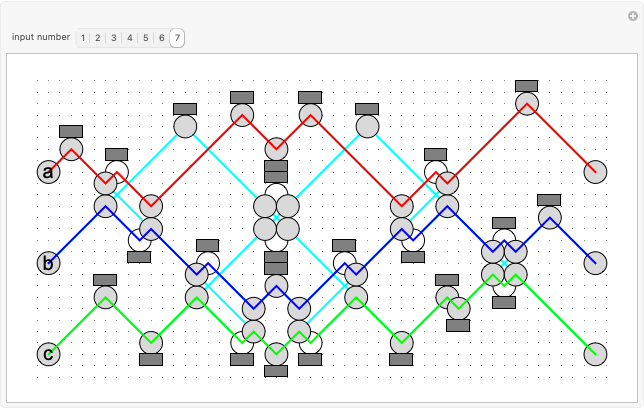
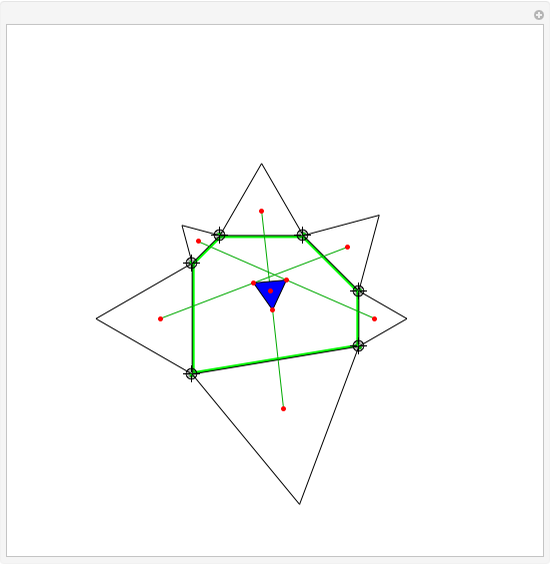
Wheel Graphs with Integer Edges

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

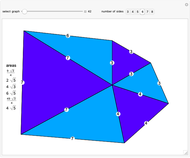
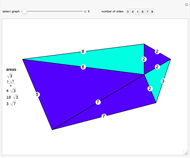
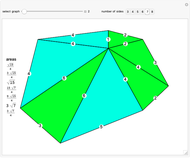
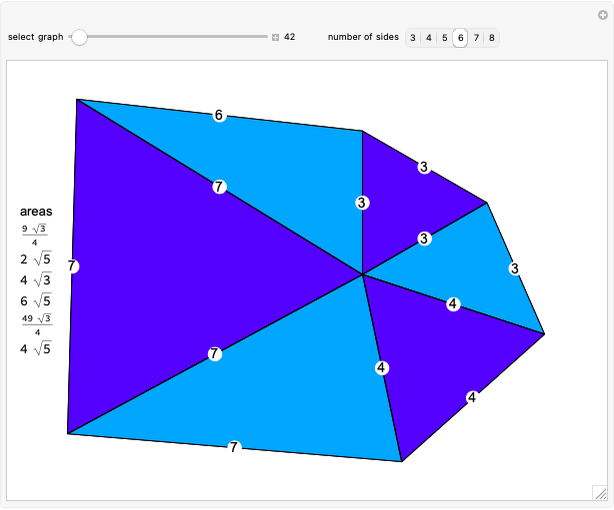
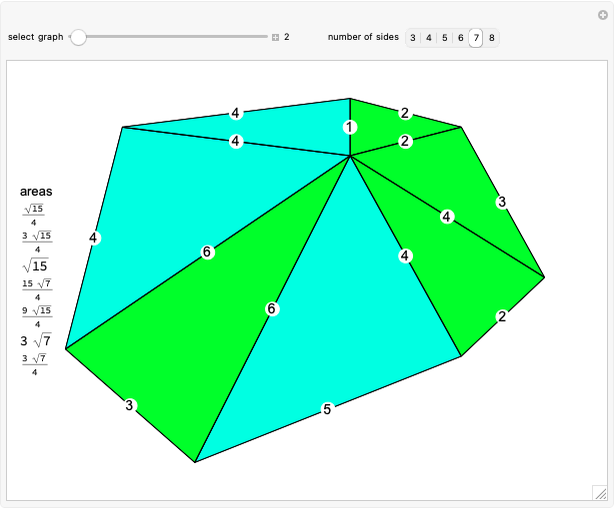
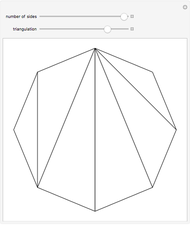
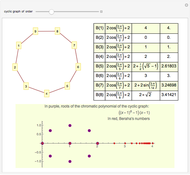
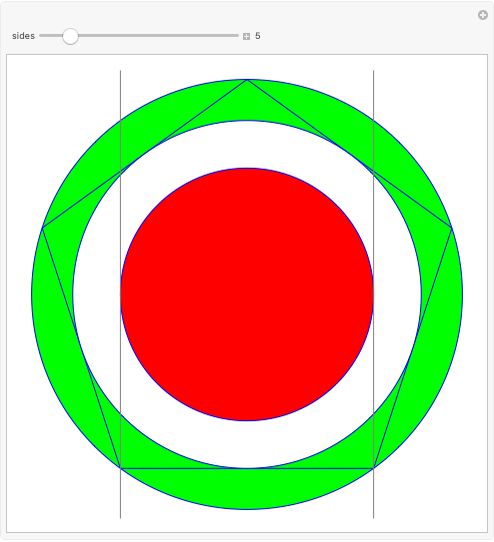
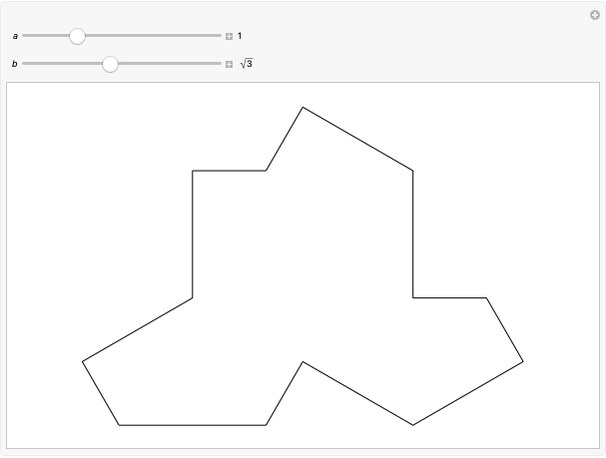
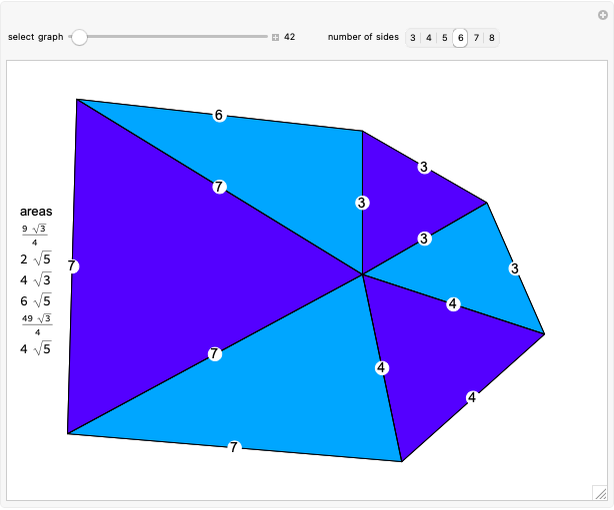
Harborth's conjecture states that the edges of any planar graph can all have integer length. Planar graphs with non-triangular faces can have edges added to get a maximal planar (or triangulated) graph, where all faces are triangles. A solution for a given maximal planar graph would contain many integer wheel graphs. This Demonstration shows many integer wheel graphs found with searches. Triangles are colored by their area radicals.

[more]

(Update for 2023). The number under the radical in a triangle area is known as the triangle's characteristic. This Demonstration seems to show that the maximum number of different triangle characteristics in an integer wheel graph is two. In 2021, Gábor Damásdi proved that an integer wheel graph can have at most two characteristics [5]. In addition, it's impossible for all the edge lengths to be odd.

[less]

Contributed by: Ed Pegg Jr (March 2015)
Open content licensed under CC BY-NC-SA

Details

Examining the 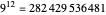hexagon possibilities took weeks, despite excluding many types of symmetries. A fast method to collect allowable heptagons, octagons, and general -gons with a given maximal edge length is currently unknown to the author.

References

[1] Wikipedia. "Harborth's Conjecture." (Mar 1, 2015) en.wikipedia.org/wiki/Harborth's_conjecture.

[2] Wikipedia. "Planar Graph." (Mar 1, 2015) en.wikipedia.org/wiki/Planar_graph# Maximal_planar _graphs.

[3] Wikipedia. "Robbins Pentagon." (Mar 1, 2015) en.wikipedia.org/wiki/Robbins_pentagon.

[4] Wikipedia. "Wheel Graph." (Mar 1, 2015) en.wikipedia.org/wiki/Wheel_graph.

[5] Gábor Damásdi, "Odd Wheels Are Not Odd-Distance Graphs." Disc. & Comp. Geom. vol 69, pp327–337, 2023. https://link.springer.com/article/10.1007/s00454-021-00325-0.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send