Constructing the Radius of a Ball
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
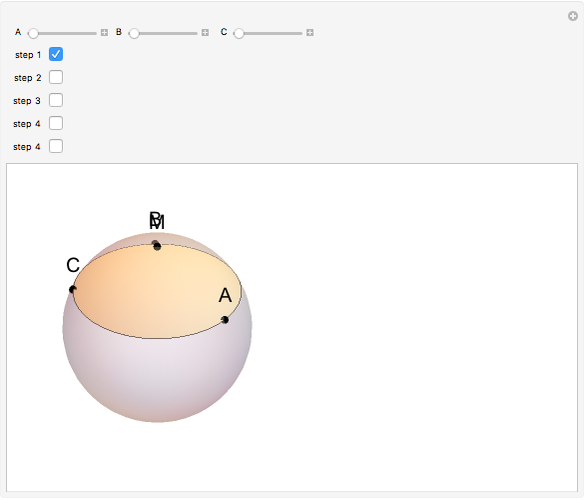
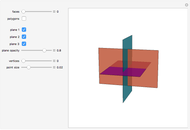
Using a ball, a sheet of paper, a compass, a straightedge without markings, and a pencil, can you draw a line segment on the paper equal to the ball's radius?
[more]
Contributed by: Izidor Hafner (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] B. A. Kordemsky, The Moscow Puzzles, London: Penguin, 1990 pp. 251–252.
Permanent Citation