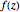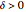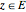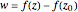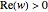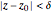Continuity of Polynomials in the Complex Plane
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
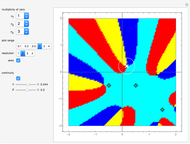
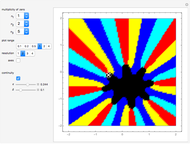
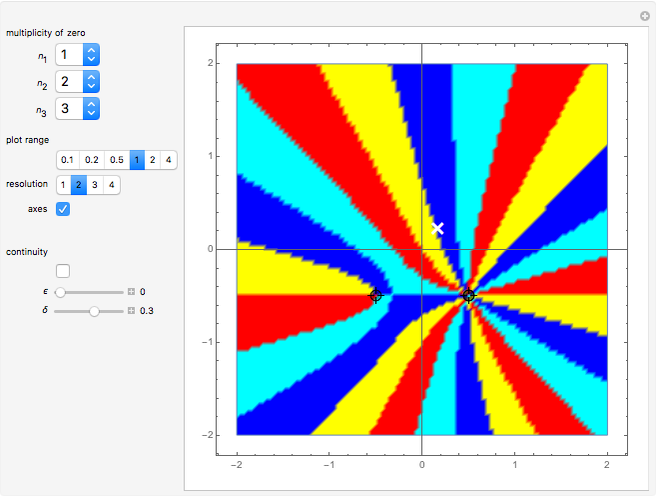
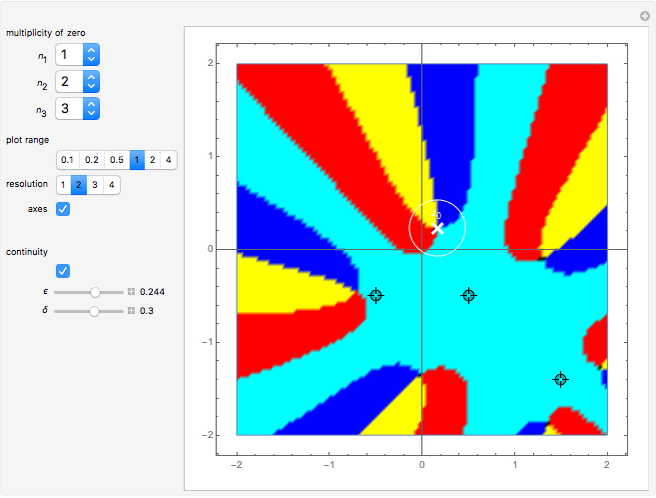
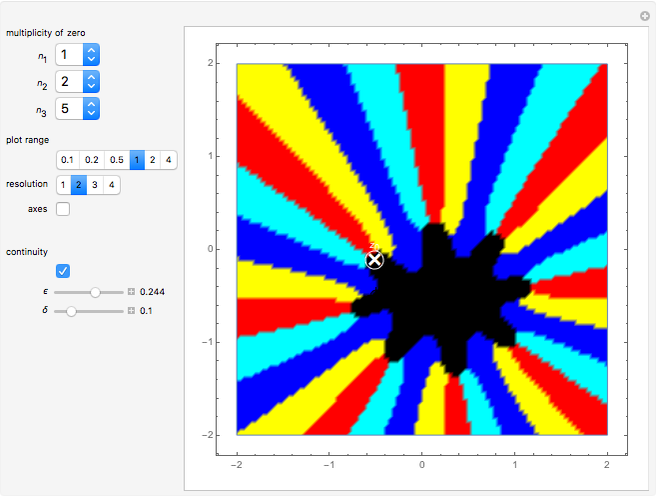
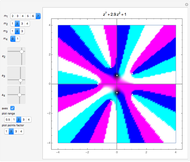
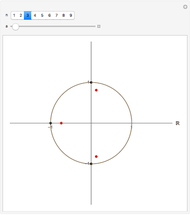
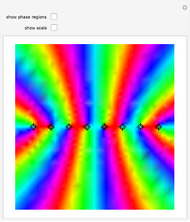
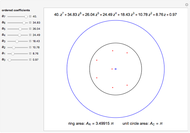
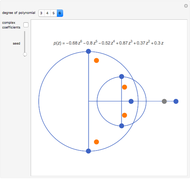
This Demonstration shows polynomials with zeros (or roots) of varying multiplicity in the complex plane. The object is to show that such a polynomial is a continuous function at a selected point 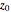 .
.
Contributed by: Izidor Hafner (March 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 pp. 35–36.
[2] A. Sveshnikov and A. Tikhonov, Theory of Functions of a Complex Variable, Moscow: Mir Publishers, 1971 pp. 24–25.
Permanent Citation