Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

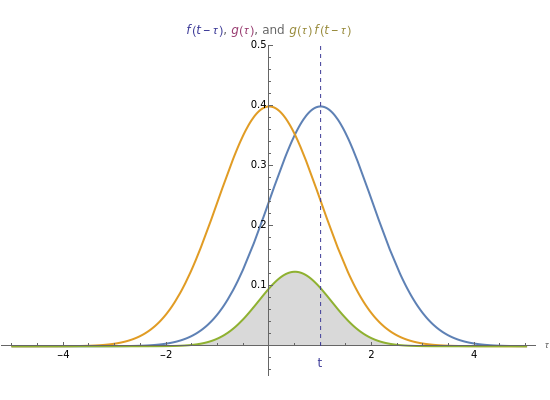
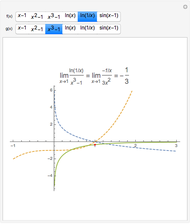
Convolution of Two Densities

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

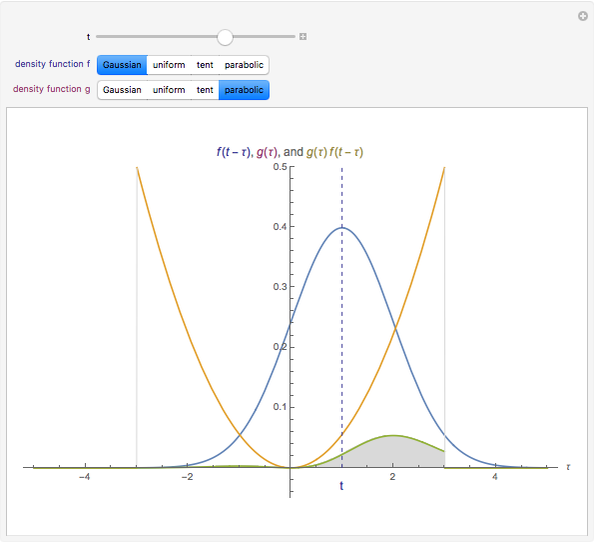
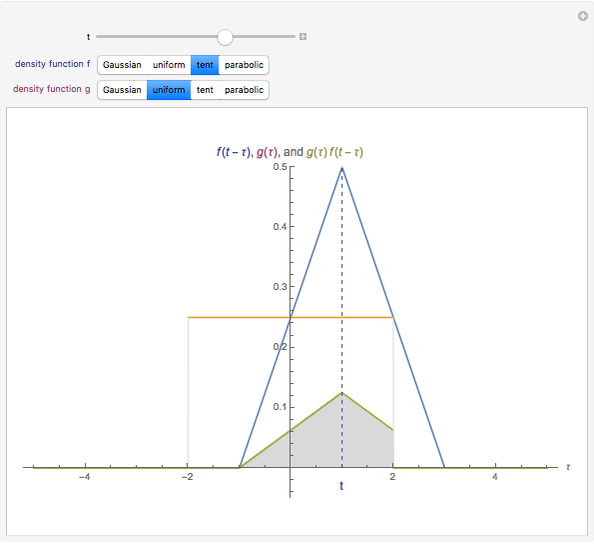
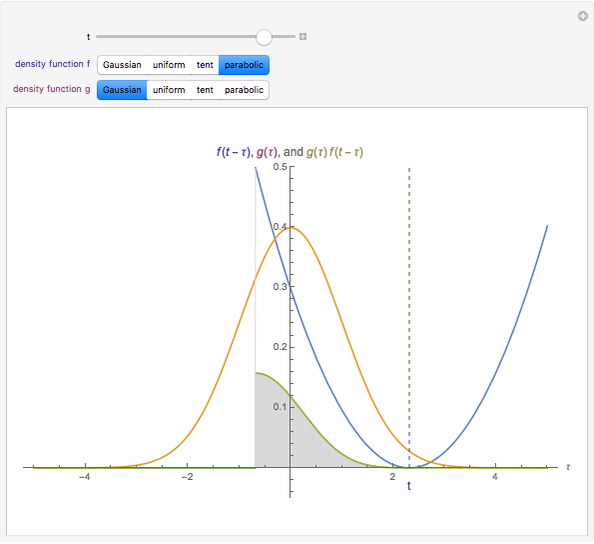
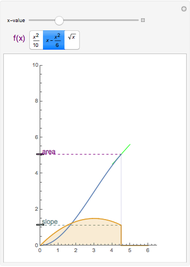
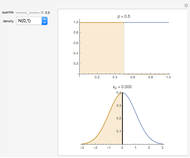
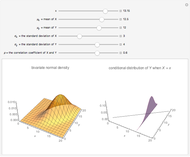
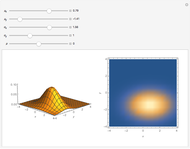
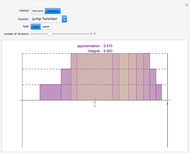
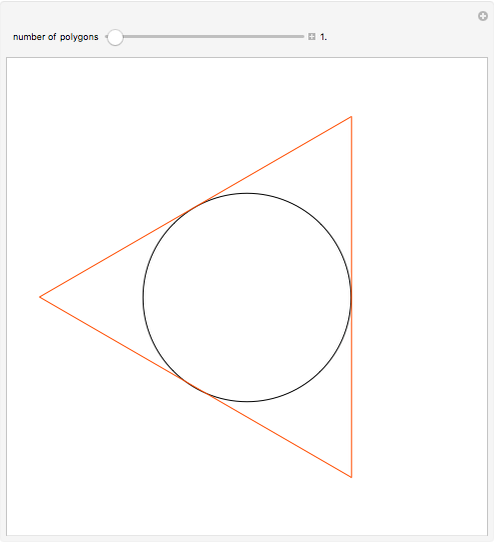
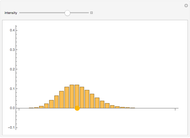
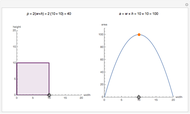
The convolution of two functions can be thought of as a measure of the overlap of the graphs as one graph is shifted horizontally across the other. Formally, if and are functions, the convolution of the two is the function .

[more]

The plot shows , that is, shifted by units, in blue, in purple, and the product of the two in gold. Thus the gray area is exactly the value of the convolution at .

If and are independent random variables with respective density functions and , then the density function of is the convolution of and . Interestingly, the convolution of two Gaussian densities is a Gaussian density.

[less]

Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send