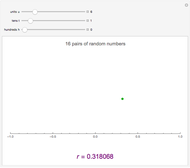
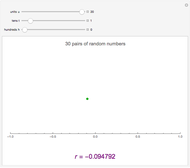
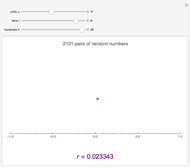
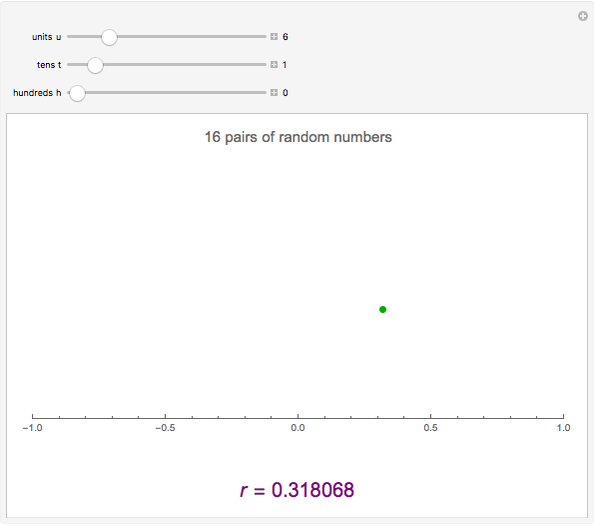
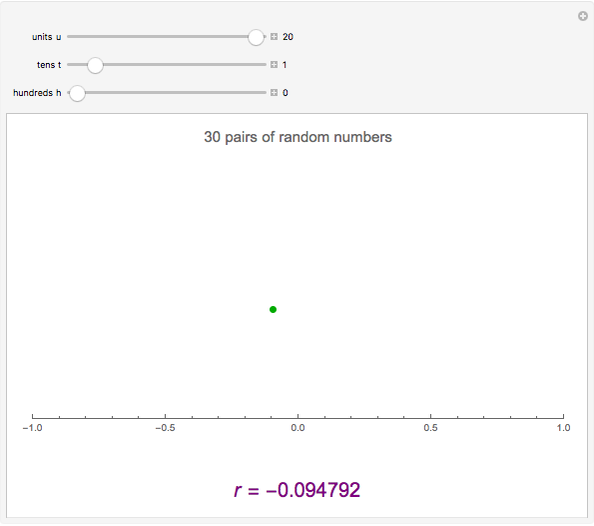
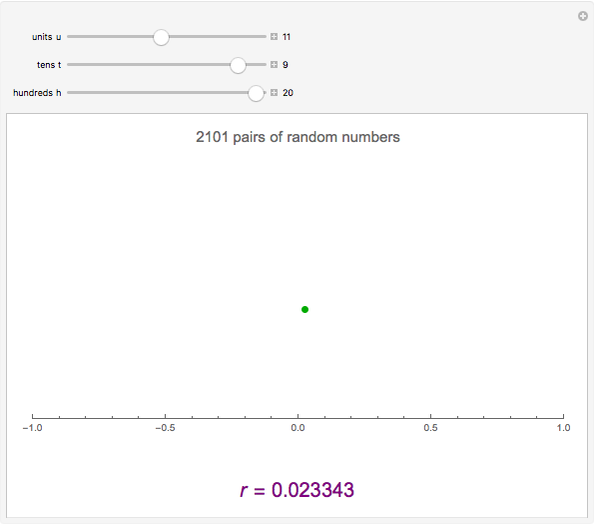
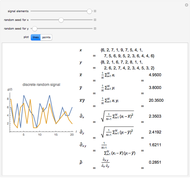
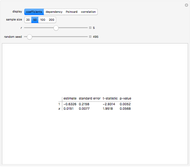
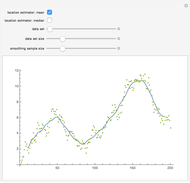
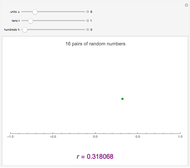
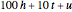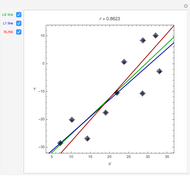
This Demonstration constructs two lists of random numbers of length and calculates the Pearson product-moment correlation coefficient as if the lists were bivariate data. For a random sample such as this, the coefficient is expected to be close to zero, with no correlation. As you increase the sample size with the sliders, the coefficient (shown with the green dot) fluctuates less and less as it floats over zero.
This computes a standard statistical quantity, the coefficient of correlation. Those studying this material for a statistics course will recognize several features in the initialization and will see how the coefficient is calculated. (The correlation can be computed directly via the built-in Mathematica function Correlation.)
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
