Cournot and Stackelberg Equilibria and Best Responses

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
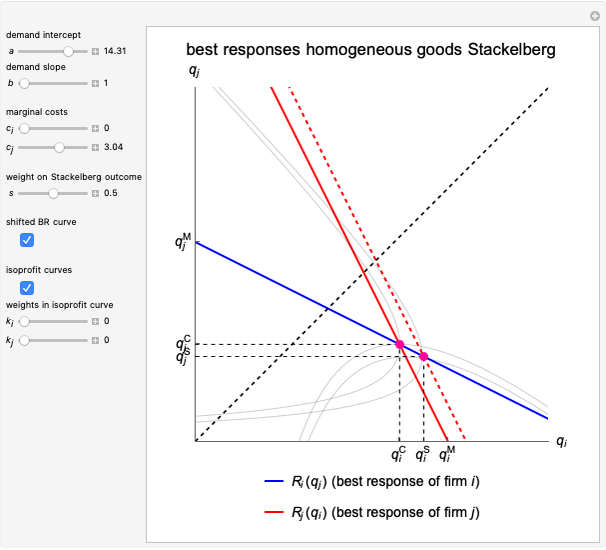
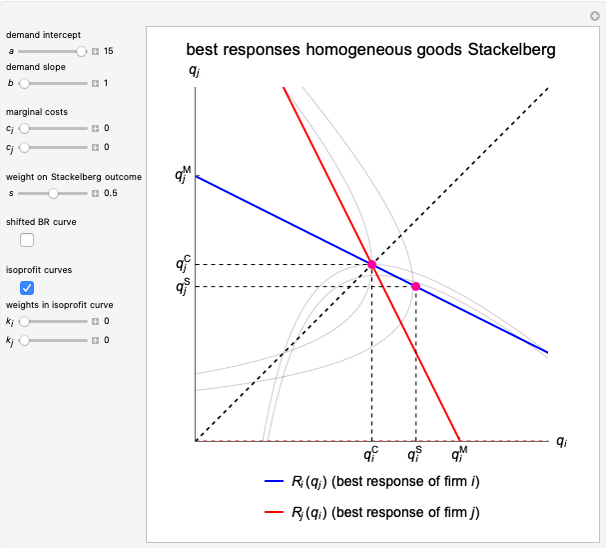
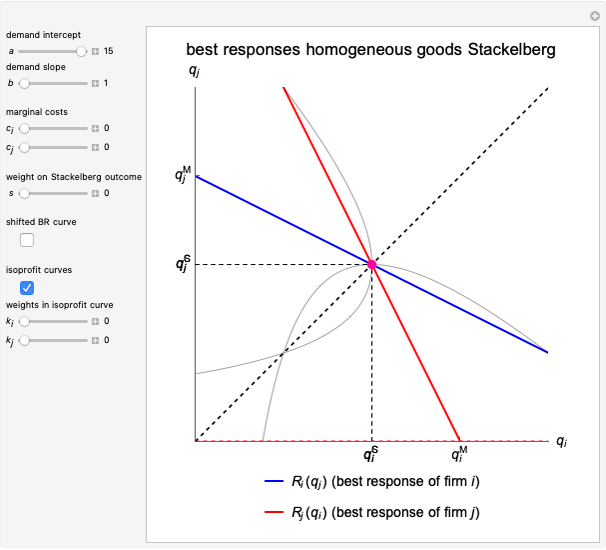
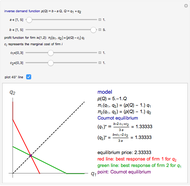
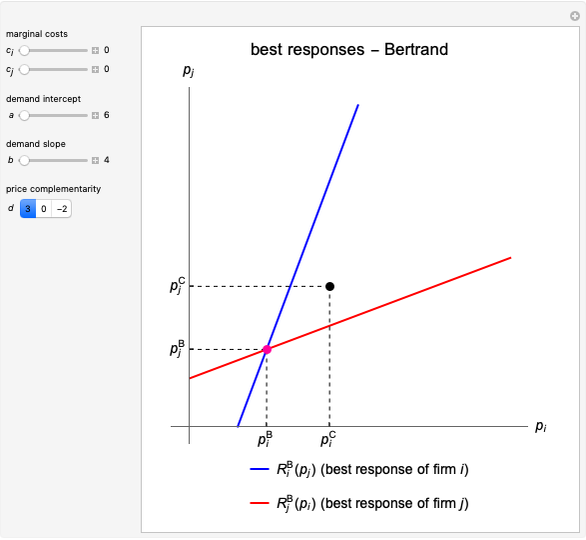
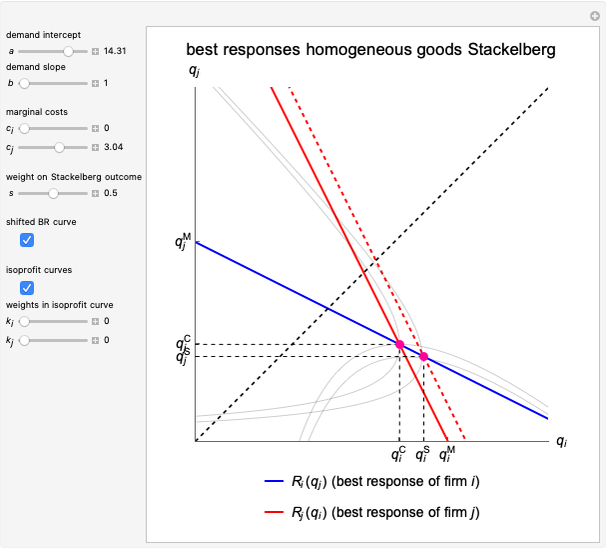
This Demonstration illustrates a number of features of the homogeneous goods Cournot and Stackelberg duopoly model [1, Chapter 4] as opposed to the Singh and Vives model of product differentiation under Bertrand competition [2], which is treated in the Duopoly Competition with Differentiated Products Demonstration. The market has inverse demand function  and the firms produce at constant marginal costs
and the firms produce at constant marginal costs 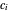 and
and  , respectively. The graph illustrates the best response curves of firm
, respectively. The graph illustrates the best response curves of firm  (blue, Stackelberg dotted) and firm
(blue, Stackelberg dotted) and firm  (red). The intersections are the Cournot equilibrium point and the Stackelberg equilibrium point. Note that the Stackelberg quantity equilibria are always below the Cournot equilibria and coincide when the weight
(red). The intersections are the Cournot equilibrium point and the Stackelberg equilibrium point. Note that the Stackelberg quantity equilibria are always below the Cournot equilibria and coincide when the weight  on the Stackelberg outcome is zero. The demand parameters are
on the Stackelberg outcome is zero. The demand parameters are 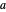 (demand intercept) and
(demand intercept) and  (demand slope). The parameters
(demand slope). The parameters 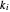 and
and 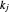 are the weights on the monopoly points in the isoprofit curves. That is, for
are the weights on the monopoly points in the isoprofit curves. That is, for 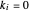 , the graph shows the isoprofit curve reached by firm
, the graph shows the isoprofit curve reached by firm  in the Cournot equilibrium. For
in the Cournot equilibrium. For 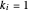 , the graph shows the isoprofit curve for firm
, the graph shows the isoprofit curve for firm  in the monopoly point, the point preferred by firm
in the monopoly point, the point preferred by firm  . The slider
. The slider  does the same for firm
does the same for firm  .
.
Contributed by: Flavio Toxvaerd (August 2022)
(University of Cambridge)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] P. Belleflamme and M. Peitz, Industrial Organization: Markets and Strategies, 2nd ed., Cambridge, UK: Cambridge University Press, 2015.
[2] N. Singh and X. Vives, "Price and Quantity Competition in a Differentiated Duopoly," The RAND Journal of Economics, 15(4), 1984 pp. 546–554.
Permanent Citation