Maximizing Profit in Ore Mining

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
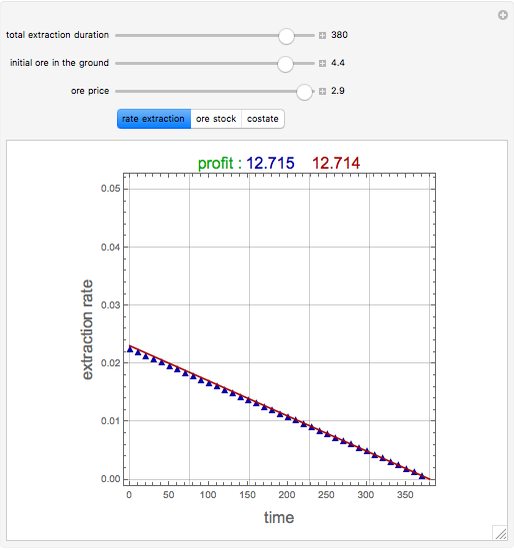
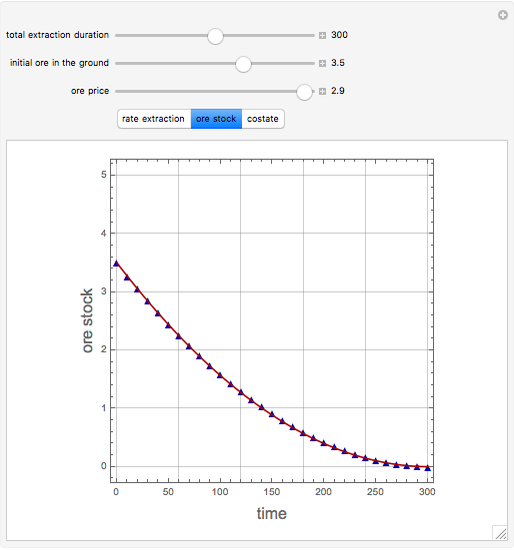
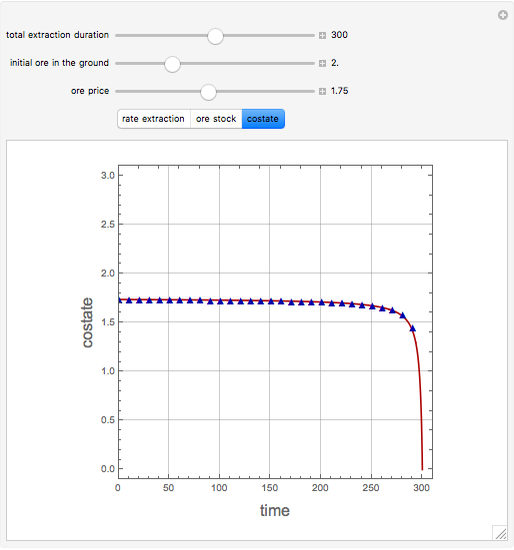
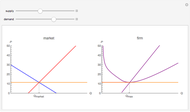
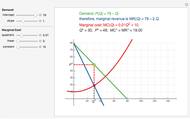
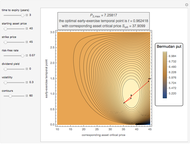
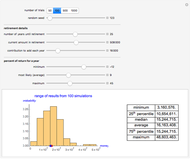
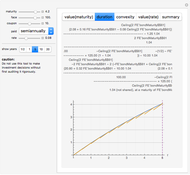
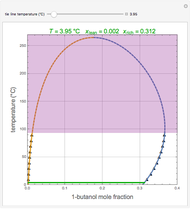
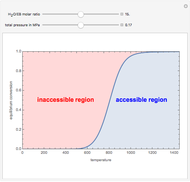
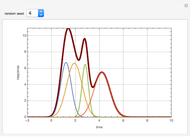
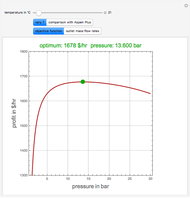
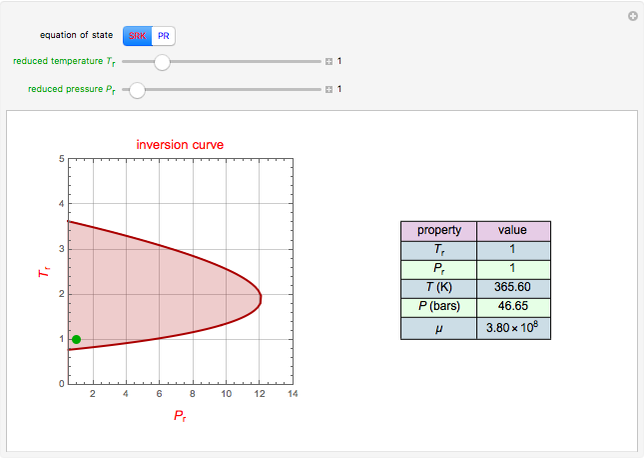
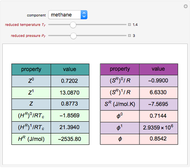
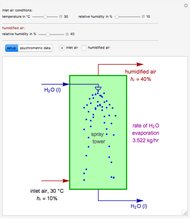
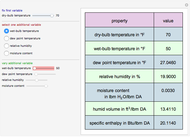
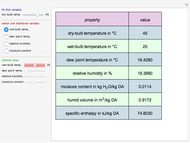
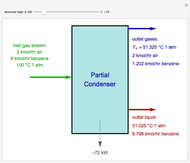
A mine owner has the right to extract ore for a time duration  . Initially there is
. Initially there is  ore in the ground. As ore is extracted, the instantaneous stock of ore
ore in the ground. As ore is extracted, the instantaneous stock of ore  declines, and
declines, and  is the extraction rate. Assume that the ore sells at a constant price
is the extraction rate. Assume that the ore sells at a constant price  and the extraction cost is
and the extraction cost is  .
.
Contributed by: Housam Binous and Ahmed Bellagi (January 2016)
(King Fahd University of Petroleum & Minerals, KSA; University of Monastir, Tunisia)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Wikipedia. "Optimal control." (Jan 25, 2016) en.wikipedia.org/wiki/Optimal_control.
Permanent Citation