Cross Ratios in the Complex Plane
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
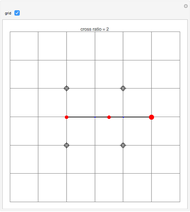
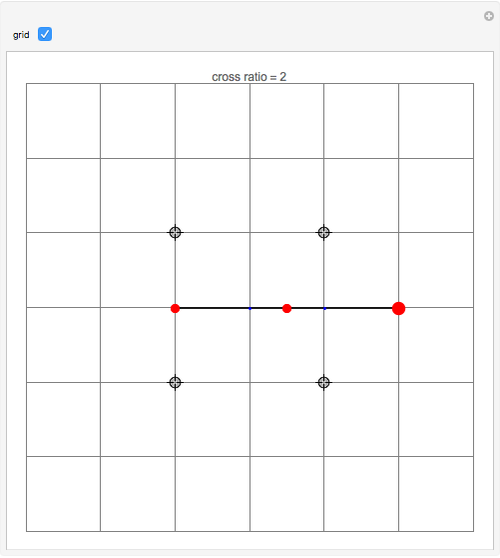
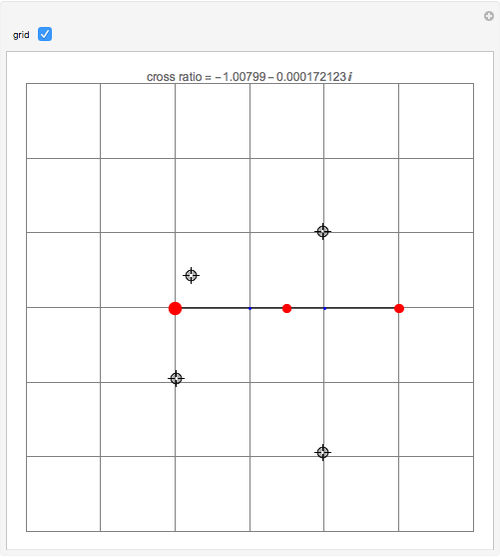
The cross ratio of four points  ,
,  ,
,  ,
,  in the extended complex plane is defined by
in the extended complex plane is defined by  , where pairs of zeros or infinities that can be canceled should be. You can drag all four locators in the graphic.
, where pairs of zeros or infinities that can be canceled should be. You can drag all four locators in the graphic.
Contributed by: George Beck (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation