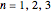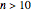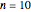Projective Planes of Low Order

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
 is shorthand for the projective plane of order
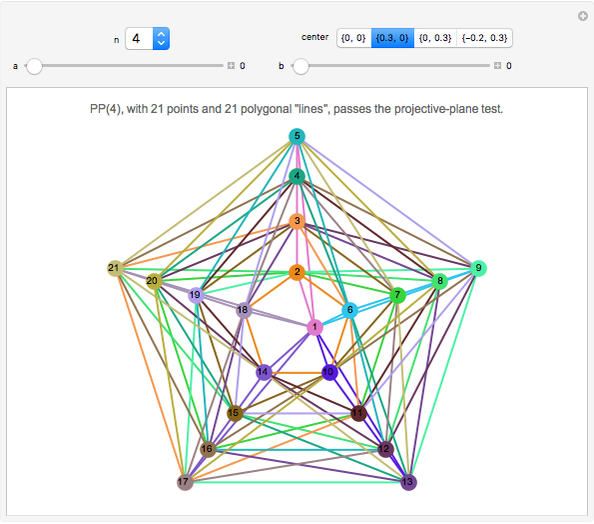
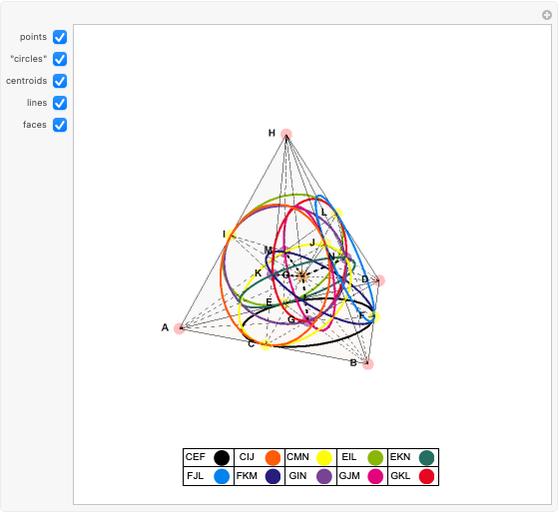
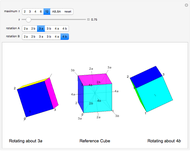
is shorthand for the projective plane of order  . The first figure presents
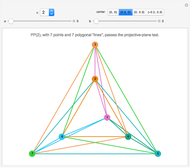
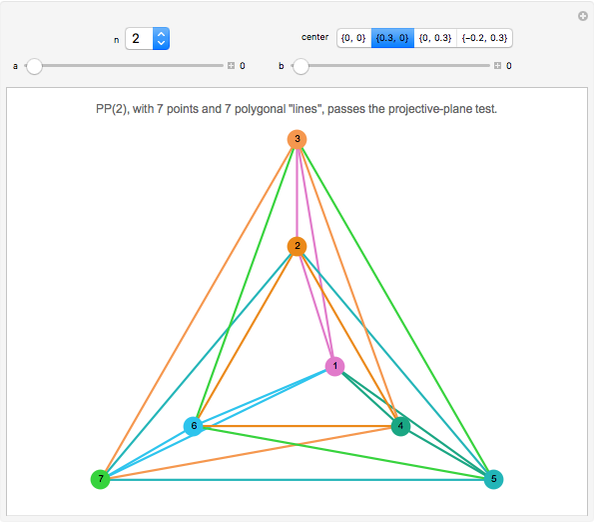
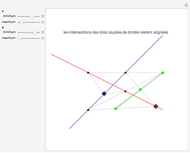
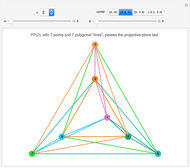
. The first figure presents  ), the best-known finite projective plane, the Fano plane, with 7 points on 7 lines. The central triangle (often drawn as a circle) is the seventh "line". Each point lies on
), the best-known finite projective plane, the Fano plane, with 7 points on 7 lines. The central triangle (often drawn as a circle) is the seventh "line". Each point lies on 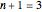 lines and each line also passes through 3 points; every pair of points defines a single line and every pair of lines defines a single point. This presentation is shown when "Fano" is selected. It does not generalize to higher orders
lines and each line also passes through 3 points; every pair of points defines a single line and every pair of lines defines a single point. This presentation is shown when "Fano" is selected. It does not generalize to higher orders  because it is a configuration, where points can be at the end or middle of a line. (The controls center,
because it is a configuration, where points can be at the end or middle of a line. (The controls center,  and
and  , do not apply in this case.) There is no difference between the two representations for
, do not apply in this case.) There is no difference between the two representations for  or "Fano" except a rearrangement of the lines.
or "Fano" except a rearrangement of the lines.
Contributed by: Roger Beresford (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The thumbnail is 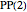 as the Fano plane with seven "lines", and shows features that are not typical of other projective planes. The first snapshot is a more representative version of
as the Fano plane with seven "lines", and shows features that are not typical of other projective planes. The first snapshot is a more representative version of 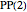 , with each "line" expanded into a triangle.
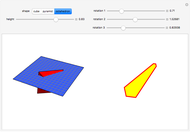
, with each "line" expanded into a triangle.  (the first prime-power case) is shown similarly. The last two snapshots show an invalid attempt to create
(the first prime-power case) is shown similarly. The last two snapshots show an invalid attempt to create  , with lines sharing two points.
, with lines sharing two points.
The  ,
, 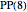 , and
, and 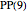 data are adapted from Projective Planes of Small Order.
data are adapted from Projective Planes of Small Order.
Projective planes are restricted cases of block designs 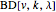 , with
, with  vertices, partitioned into blocks (sets of
vertices, partitioned into blocks (sets of  vertices) in such a way that any two vertices are in exactly
vertices) in such a way that any two vertices are in exactly  blocks.
blocks.  (if it exists) is
(if it exists) is  . A configuration
. A configuration  is
is  points each on exactly
points each on exactly  lines; points and lines can be at infinity; only
lines; points and lines can be at infinity; only  ,
,  , and
, and 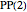 allow a configuration.
allow a configuration. 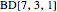 , configuration
, configuration  , and the Fano plane all define
, and the Fano plane all define 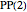 .
.
Permanent Citation