Cyclic Voltammetry Corrupted by Ohmic Drop

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
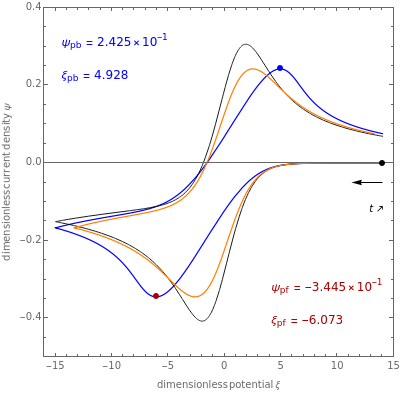
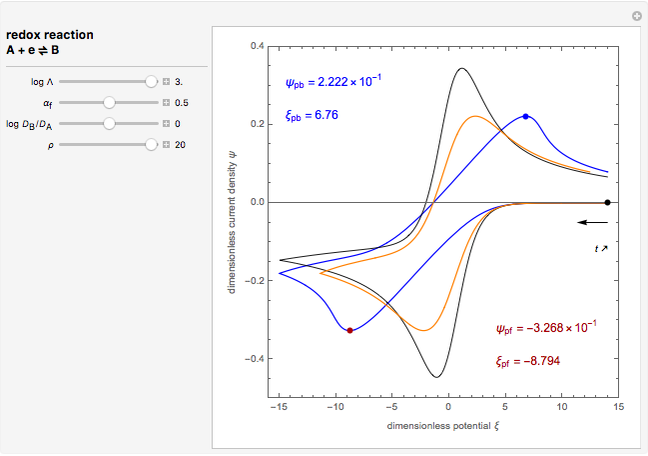
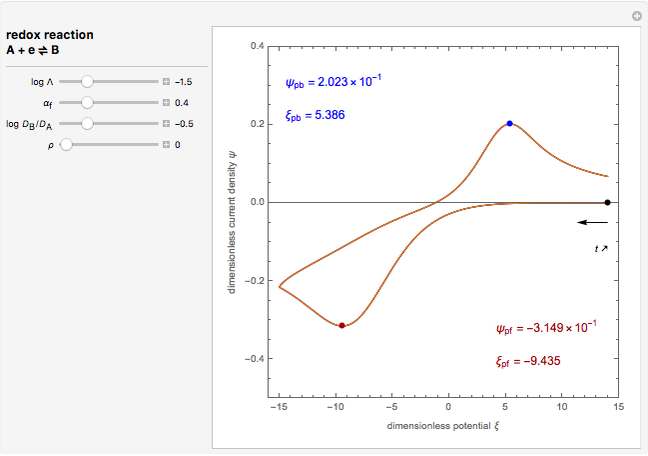
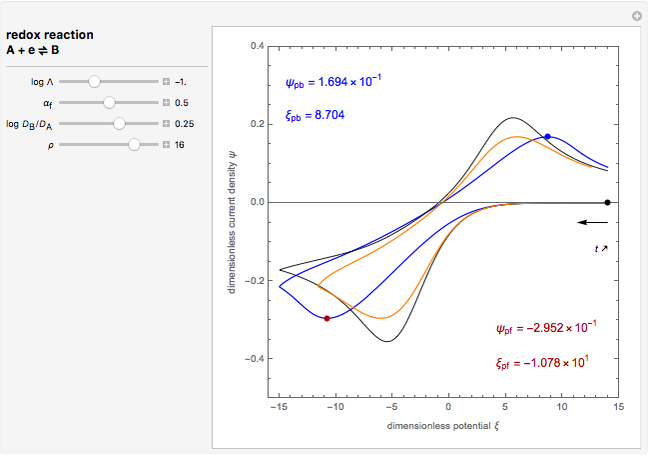
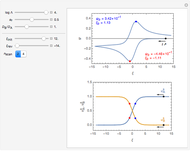
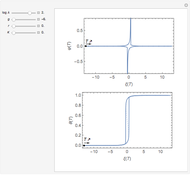
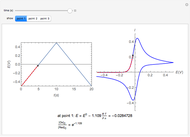
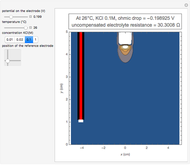
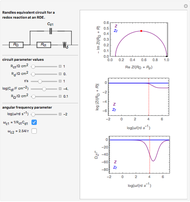
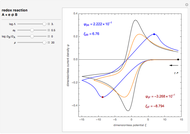
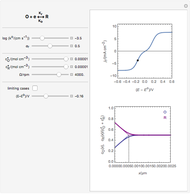
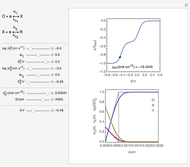
This Demonstration models the undesirable effect of the uncompensated resistance of the electrolyte on the cyclic voltammogram of a redox reaction ( ) involving soluble species. The black line is the ideal voltammogram plotted without ohmic drop. The ohmic drop describes the overpotential due to the current flow in the electrolyte. The blue line is the voltammogram corrupted by ohmic drop. The orange line is the voltammogram obtained from the blue line when the electrode potential is numerically corrected for ohmic drop. You can experiment with the effects of electron transfer kinetics, mass transport and ohmic drop using the controls for the dimensionless parameters. The plots show the dimensionless current density
) involving soluble species. The black line is the ideal voltammogram plotted without ohmic drop. The ohmic drop describes the overpotential due to the current flow in the electrolyte. The blue line is the voltammogram corrupted by ohmic drop. The orange line is the voltammogram obtained from the blue line when the electrode potential is numerically corrected for ohmic drop. You can experiment with the effects of electron transfer kinetics, mass transport and ohmic drop using the controls for the dimensionless parameters. The plots show the dimensionless current density  as a function of the dimensionless potential
as a function of the dimensionless potential  .
.
Contributed by: Claude Montella and Jean-Paul Diard (May 2017)
Univ. Grenoble Alpes, LEPMI, Grenoble, France
Open content licensed under CC BY-NC-SA
Snapshots
Details
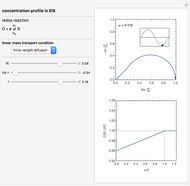
This Demonstration focuses on a one-step redox reaction ( ) involving two soluble species
) involving two soluble species  and
and  , taking place at the surface of a planar macroelectrode. Mass transport of both species is characterized as one-dimensional semi-infinite diffusion in the unstirred electrolyte. The initial concentration of species
, taking place at the surface of a planar macroelectrode. Mass transport of both species is characterized as one-dimensional semi-infinite diffusion in the unstirred electrolyte. The initial concentration of species  is null. Because of the uncompensated resistance of the electrolyte, the variation of the electrode potential versus time is not linear, and the cyclic voltammogram differs from the ideal curve plotted without ohmic drop. In addition, correction of voltammetric data, a posteriori, is not the appropriate method to recover the ideal voltammogram.
is null. Because of the uncompensated resistance of the electrolyte, the variation of the electrode potential versus time is not linear, and the cyclic voltammogram differs from the ideal curve plotted without ohmic drop. In addition, correction of voltammetric data, a posteriori, is not the appropriate method to recover the ideal voltammogram.
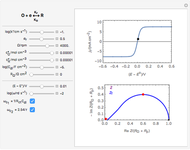
Dimensionless notation is used for the sake of generality, defining  ,
,  ,
,  and
and  . Here
. Here  is the standard rate constant (
is the standard rate constant ( ) of the electrochemical reaction
) of the electrochemical reaction  , all symbols having their usual meaning;
, all symbols having their usual meaning;  is the symmetry factor for electron transfer in the forward direction (here reduction direction);
is the symmetry factor for electron transfer in the forward direction (here reduction direction);  is the potential scan rate in V/s;
is the potential scan rate in V/s;  and
and  are the diffusion coefficients of redox species in
are the diffusion coefficients of redox species in  ;
;  is the Faradaic current density in A/
is the Faradaic current density in A/ ;
;  is the electrode surface area in
is the electrode surface area in  ;
;  is the uncompensated resistance in
is the uncompensated resistance in  ;
;  is the controlled potential (with linear variation with respect to time); and
is the controlled potential (with linear variation with respect to time); and  is the formal potential of redox couple, both potentials being given in V versus the reference electrode. Because of the uncompensated resistance
is the formal potential of redox couple, both potentials being given in V versus the reference electrode. Because of the uncompensated resistance  , the effective potential applied to the electrode is
, the effective potential applied to the electrode is  . Its deviation from the controlled potential
. Its deviation from the controlled potential  is linearly proportional to the current flowing through the electrode.
is linearly proportional to the current flowing through the electrode.
The numerical solution of the diffusion equations, together with the boundary condition (electrochemical kinetics) at the electrolyte/electrode interface and the bulk conditions (constant concentrations with respect to time), is readily obtained using the so-called method of lines implemented in the built-in Mathematica function NDSolve. The dimensionless current density  is computed versus time from the dimensionless flux of redox species at the interface. The cyclic voltammogram is the parametric plot of
is computed versus time from the dimensionless flux of redox species at the interface. The cyclic voltammogram is the parametric plot of  versus the dimensionless potential
versus the dimensionless potential  . You can vary the parameter
. You can vary the parameter  , the diffusion coefficient ratio
, the diffusion coefficient ratio 

 (in logarithmic scales) and the symmetry factor
(in logarithmic scales) and the symmetry factor  , as well as the dimensionless resistance
, as well as the dimensionless resistance  .
.
The dimensionless coordinates of voltammetric peaks are evaluated in both the reduction (forward scan) and oxidation (reverse scan) directions, whenever such peaks exist.
Reference
[1] A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed., New York: Wiley, 2001.
Permanent Citation