Cyclogons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
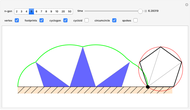
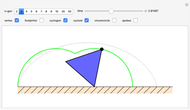
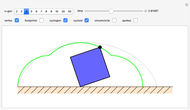
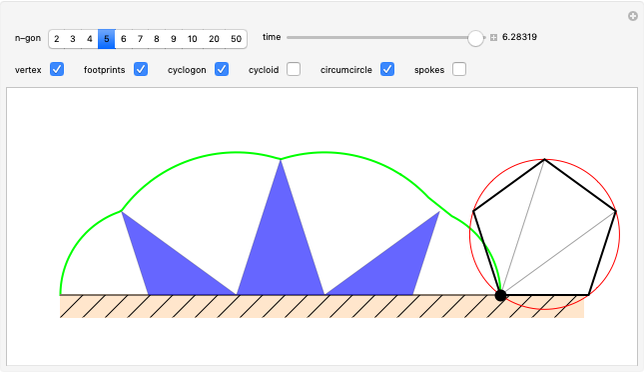
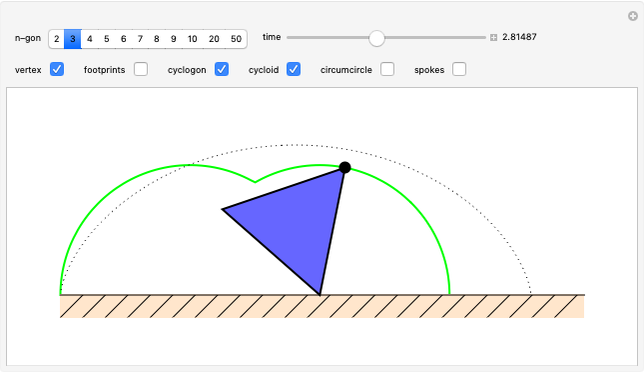
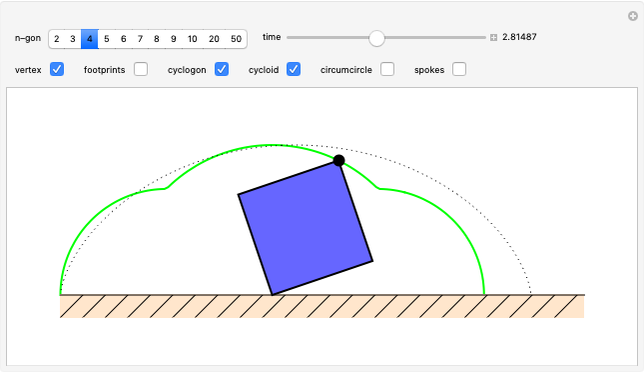
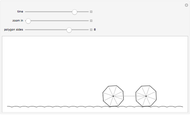
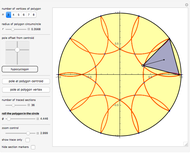
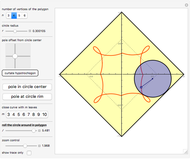
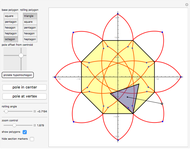
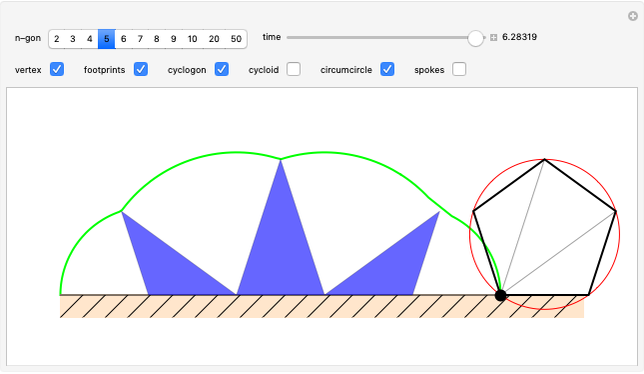
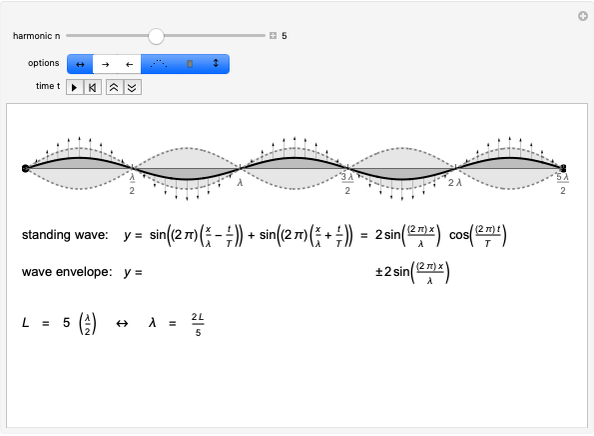
A vertex of a rolling regular polygon traces out a cyclogon. Roll the polygon to see the alternating circular sectors and triangular "footprints" that form the polygon. Vary the number of sides of the polygon, showing visually that the cyclogon becomes a cycloid in the limit as the number of sides increases.
Contributed by: Kenneth E. Caviness (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
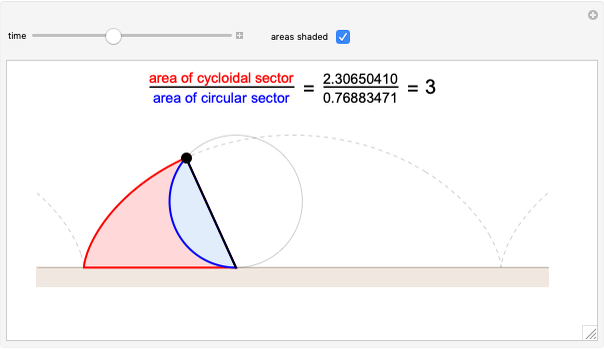
A cyclogon, the path of a vertex of a regular polygon rolling along a line without slipping, is made up of a repeating pattern of arches, each arch consisting of a series of circular arcs of radii equal to the lengths of the various diagonals of the polygon. It has been shown that the area under a single arch of the cyclogon is equal to the sum of the area of the polygon and twice the area of its circumscribed circle. This Demonstration gives an animated view of the rolling polygon and the formation of the cyclogon curve and the triangular "footprints" under the curve, showing that the sum of the footprint areas is equal to the area of the polygon.
For the entire proof, including treatment of the areas of the circular sectors that alternate with the footprint triangles, see [1, 2].
Vary the number of sides of the polygon, show or hide the footprint triangles, the tracing vertex, the circle circumscribing the polygon, the cycloid of the circle, and the cyclogon itself. The spokes of the  -sided polygon divide it into
-sided polygon divide it into  identical isosceles triangles, each with central angle
identical isosceles triangles, each with central angle  . This is also the angle the polygon rotates between vertical positions and the angle of each circular sector under the cyclogon.
. This is also the angle the polygon rotates between vertical positions and the angle of each circular sector under the cyclogon.
In the limit, as the number of sides grows without bound, the cyclogon becomes a cycloid, and the result reduces to the classic theorem that the area under one arch of a cycloid is equal to three times the area of its generating circle.
But the relationship holds even if the number of sides is set equal to 2, extending the validity of the theorem in the other direction: A "polygon" of two sides of length  has no area, the circumscribed circle has diameter
has no area, the circumscribed circle has diameter  and area
and area  , and a single arch of its cyclogon has the semi-circular area
, and a single arch of its cyclogon has the semi-circular area  . Thus for the
. Thus for the  case as well, the area under an arch of the cyclogon is equal to twice the area of the circumscribed circle plus the area of the polygon.
case as well, the area under an arch of the cyclogon is equal to twice the area of the circumscribed circle plus the area of the polygon.
The code contains an explicit parametric form expression for the cyclogon, derived here for perhaps the first time. The code for the rolling polygon itself was inspired by and based on "Rolling Polygons" by Jaime Rangel-Mondragon. (See the Related Links reference below.)
References
[1] T. M. Apostol and M. A. Mnatsakanian, New Horizons in Geometry, Washington, D.C.: MAA Mathematical Association of America, 2012.
[2] T. M. Apostol and M. A. Mnatsakanian, "Cycloidal Areas without Calculus," Math Horizons, 7(1), 1999 pp. 12–16.
Permanent Citation