pq-System Explorer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
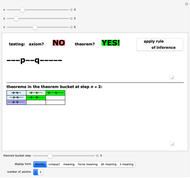
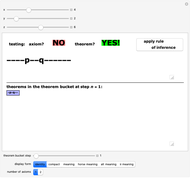
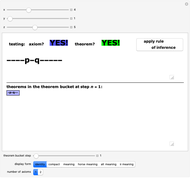
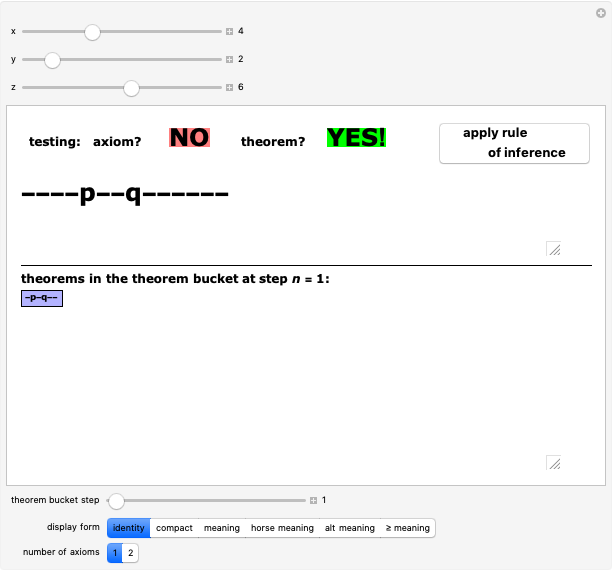
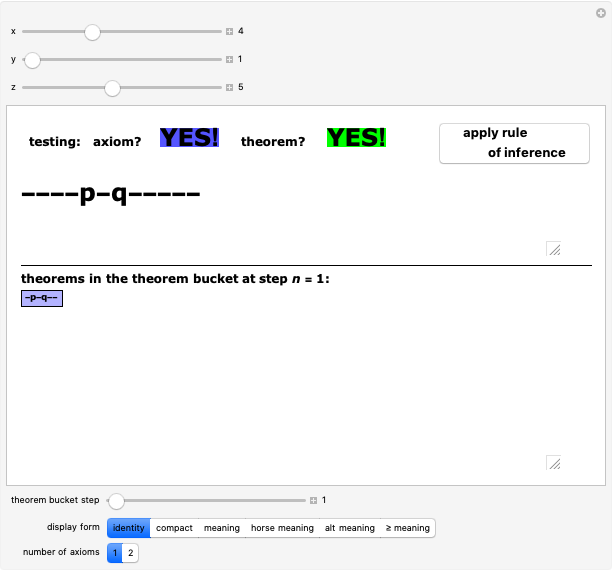
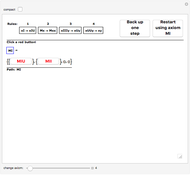
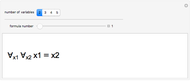
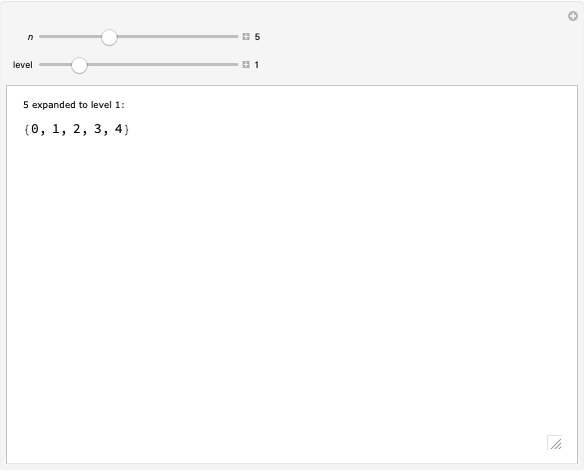
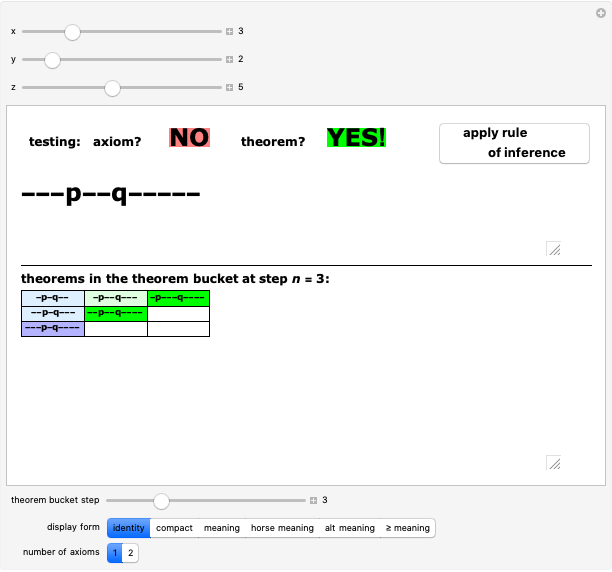
The pq-system [1] is a formal system in which theorems can be derived or generated from axioms or from other theorems by using a rule of inference. Use only the upper sliders to adjust the "pq-string" and test whether it is an axiom or a theorem or neither. (Axioms must follow the axiom schema or pattern  , where
, where  represents a string of hyphens.) This Demonstration is a power tool for exploring this sample formal system, but the exploration process occurs in your own mind: do not use the lower slider or buttons until you have thoroughly explored the system or you short-circuit the process! (Details below.)
represents a string of hyphens.) This Demonstration is a power tool for exploring this sample formal system, but the exploration process occurs in your own mind: do not use the lower slider or buttons until you have thoroughly explored the system or you short-circuit the process! (Details below.)
Contributed by: Kenneth E. Caviness (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration allows you to explore the pq-system [1], an example formal system introduced by Douglas Hofstadter in Chapter 2 of Gödel, Escher, Bach as a means of illustrating the important elements of formal systems (axioms, theorems, rules of inference), the mechanical and intelligent modes of treating a formal system, and the concept of a decision procedure. The system has an infinite number of axioms that all follow the axiom schema or pattern,  (where
(where  represents a string of hyphens). There is only one rule of inference: if
represents a string of hyphens). There is only one rule of inference: if  is a theorem or an axiom, then
is a theorem or an axiom, then  is also a theorem of the system.
is also a theorem of the system.
The upper sliders facilitate the M-mode exploration of the system, helping you to become familiar with its axioms and theorems. Once you find an axiom or theorem, clicking the "apply rule of inference" button automatically adjusts the sliders to generate another theorem. This eliminates much of the drudgery of M-mode investigation for the human researcher and results in an easier transition to  -mode (i.e., jumping outside the system and thinking about it), perhaps discovering a decision procedure—a test for theoremhood that immediately distinguishes theorems from non-theorems without generating all the theorems mechanically. Using the lower controls is strongly discouraged until you play with the system for a while using the upper controls: it would give away answers that you should figure out yourself! You should also try to find a decision procedure now before reading farther in these notes.
-mode (i.e., jumping outside the system and thinking about it), perhaps discovering a decision procedure—a test for theoremhood that immediately distinguishes theorems from non-theorems without generating all the theorems mechanically. Using the lower controls is strongly discouraged until you play with the system for a while using the upper controls: it would give away answers that you should figure out yourself! You should also try to find a decision procedure now before reading farther in these notes.
It is immediately clear that the only strings ever generated will consist of three sequences of hyphens separated by exactly one  and exactly one
and exactly one  (in that order). These are called well-formed strings, but not all such strings are theorems. After playing with the system awhile, you will almost certainly start to see other patterns as well. If you are still drawing a blank, click the "compact" button to study the system in a different light. The "meaning" button will confirm the decision procedure that you have probably already figured out for yourself at this point.
(in that order). These are called well-formed strings, but not all such strings are theorems. After playing with the system awhile, you will almost certainly start to see other patterns as well. If you are still drawing a blank, click the "compact" button to study the system in a different light. The "meaning" button will confirm the decision procedure that you have probably already figured out for yourself at this point.
Lest you think that the "meaning" is implicit in the formal system, Hofstadter gives two alternative translations, which may be meaningful for horses and humans, respectively: the next two buttons show these. It is extremely interesting to consider alternative (meaningful?) translations of a formal system (which in itself originally seems meaningless).
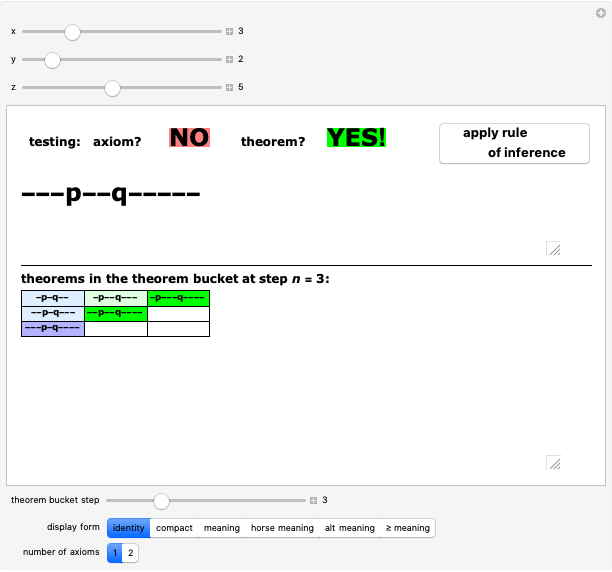
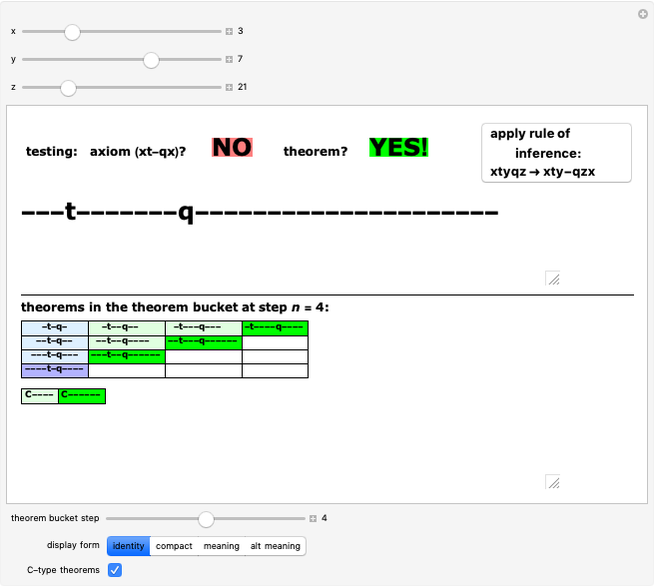
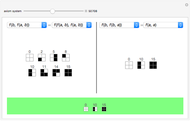
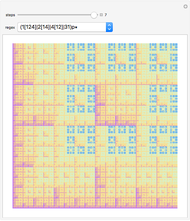
Unlike the MIU-system (see Related Links), whose rules of inference sometimes lengthen and sometimes shorten the strings, in the pq-system the single inference rule generates longer and longer (well-formed) strings. This guarantees the existence of a decision procedure: at worst, we can recursively iterate backwards from a given well-formed string to the string from which it must have been generated until a string is reached that either is an axiom or is not a well-formed string. This is the algorithm used here to test the  -strings. (But there is a simple alternative, shown by the "meaning" button, a shortcut used here to activate/deactivate the button to generate new theorems.) Hofstadter also presents an algorithm guaranteed to generate a list of all possible axioms and theorems of the system, starting at step 1 by putting the simplest axiom into our collection of known theorems (the "theorem bucket"), then at each subsequent step adding the next axiom to the bucket and all new strings that are generated from those already in the bucket. The lower panel illustrates this method, with the "theorem bucket step" slider showing the new axiom and theorems in a deeper color than those found in previous steps. If this procedure is continued, it will eventually come to any axiom and to any theorem of the pq-system.
-strings. (But there is a simple alternative, shown by the "meaning" button, a shortcut used here to activate/deactivate the button to generate new theorems.) Hofstadter also presents an algorithm guaranteed to generate a list of all possible axioms and theorems of the system, starting at step 1 by putting the simplest axiom into our collection of known theorems (the "theorem bucket"), then at each subsequent step adding the next axiom to the bucket and all new strings that are generated from those already in the bucket. The lower panel illustrates this method, with the "theorem bucket step" slider showing the new axiom and theorems in a deeper color than those found in previous steps. If this procedure is continued, it will eventually come to any axiom and to any theorem of the pq-system.
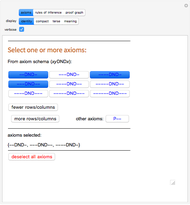
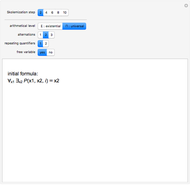
In Chapter 4 of his book, Hofstadter modifies the pq-system by introducing a second axiom schema,  . This modified system can be studied by setting the "number of axioms" control to 2. Many well-formed strings are now identified as axioms or theorems that were not in the original system. The theorem bucket is also updated: one axiom of each type is added at each step, and again all newly constructed theorems are shown. Interestingly enough, the logical system is now inconsistent with our previous meanings: many theorems now make false statements if shown in "meaning" or "alt meaning" display modes. The user may wish to spend some time looking for a valid meaning for the modified system before pushing the "≥ meaning" button, which again shows the theorems of the system as representing true arithmetic statements. However this matching of form and meaning is incomplete: although the theorems again only translate as true statements about positive integers, not all true statements using these symbols are theorems of the system.
. This modified system can be studied by setting the "number of axioms" control to 2. Many well-formed strings are now identified as axioms or theorems that were not in the original system. The theorem bucket is also updated: one axiom of each type is added at each step, and again all newly constructed theorems are shown. Interestingly enough, the logical system is now inconsistent with our previous meanings: many theorems now make false statements if shown in "meaning" or "alt meaning" display modes. The user may wish to spend some time looking for a valid meaning for the modified system before pushing the "≥ meaning" button, which again shows the theorems of the system as representing true arithmetic statements. However this matching of form and meaning is incomplete: although the theorems again only translate as true statements about positive integers, not all true statements using these symbols are theorems of the system.
References:
[1] D. R. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, New York: Basic Books, 1979.
Permanent Citation