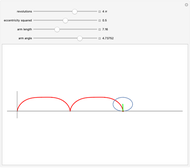
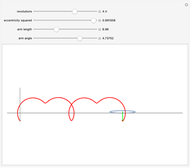
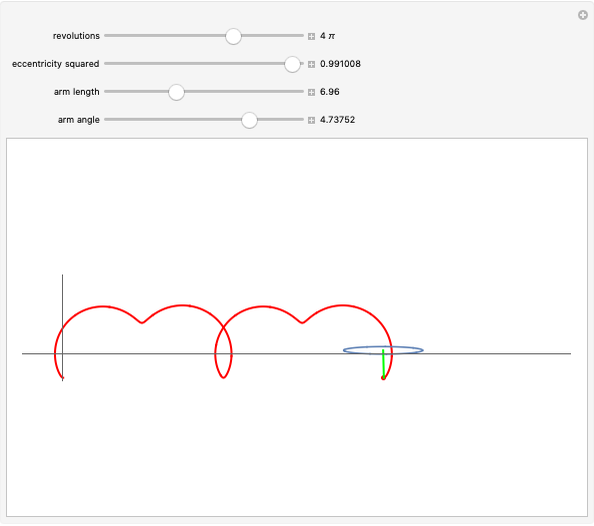
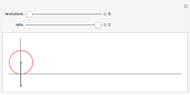
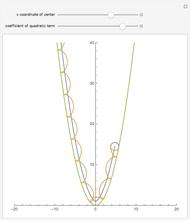
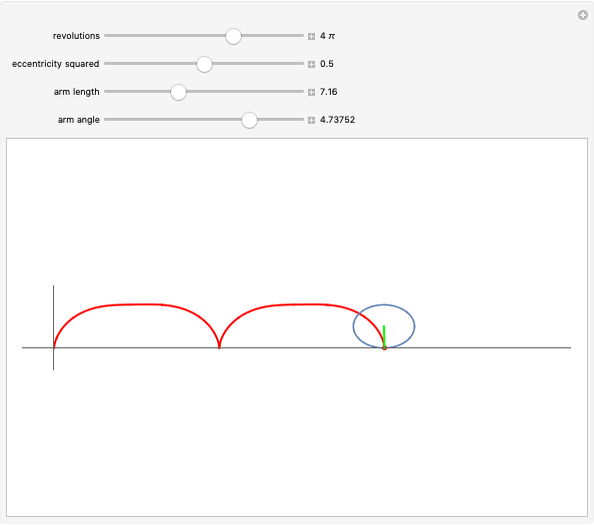
As a circle rolls along a straight line, a point on the circle's rim traces a curve called a cycloid. Variations occur if the point is inside the circle or outside on an arm attached to the circle. This Demonstration extends these variations by allowing the circle to have nonzero eccentricity, that is, the circle is replaced by a rolling ellipse. The fixed point can be moved off the ellipse's perimeter by adjusting the length of the radial arm, yielding elliptical analogues of the curtate cycloid (fixed point inside perimeter) and prolate cycloid (fixed point outside perimeter).