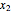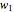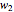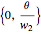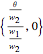Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Delta and Perceptron Training Rules for Neuron Training

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

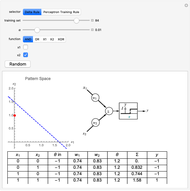
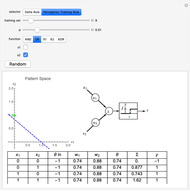
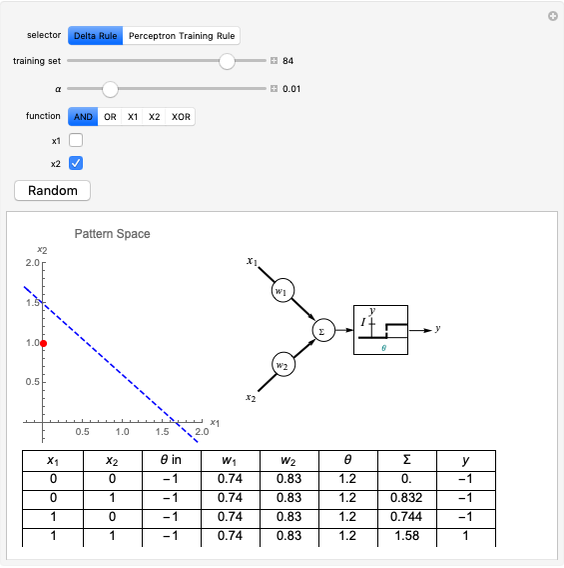
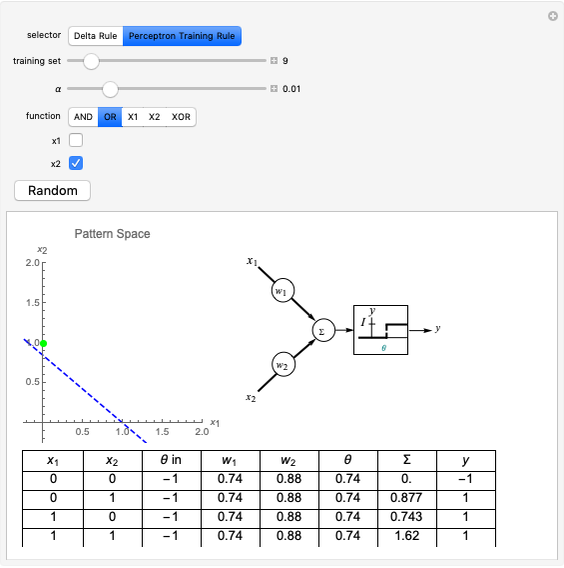
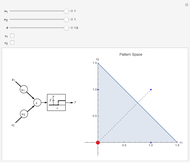
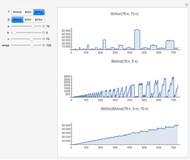
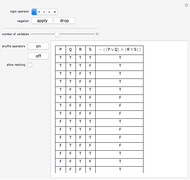
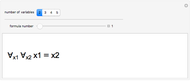
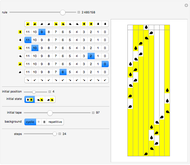
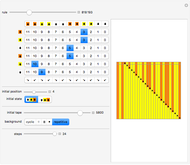
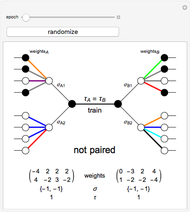
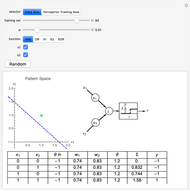
This Demonstration shows how a single neuron is trained to perform simple linear functions in the form of logic functions (AND, OR, X1, X2) and its inability to do that for a nonlinear function (XOR) using either the "delta rule" or the "perceptron training rule".

[more]

Select the logic function to be trained on the perceptron. As you vary the training set, the plot and table are updated to show the current weights, decision line, and how the function would be evaluated according to the perceptron's state. You can adjust the learning rate with the parameter . The "Random" button randomizes the weights so that the perceptron can learn from scratch.

The inputs can be set on and off with the checkboxes. The dot representing the input coordinates is green or red as the function evaluates to true or false, respectively.

The diagram on the right shows the connections between the inputs ( and ), weights ( and ), and threshold ().

The current logic table is shown in the table below the graph with inputs and and output .

The pattern space is the area in which the neuron is defined. This area represents the different possibilities that can occur for different inputs. The decision line, the horizon from which the function is evaluated as true or false, is calculated from the -intercepts and .

As more training sets are passed through the perceptron (as you move the slider to the right) the perceptron learns the behavior expected from it. If the perceptron does not converge to a desired solution, reset the weights and try again. The exception is the XOR function, which will never converge as it is not a linearly separable function.

[less]

Contributed by: Hector Sanchez (July 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Delta rule: When the neuron is trained via the delta rule, the algorithm is:

1. Evaluate the network according to the equation: .

2. If the current output 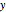is already equal to the desired output , repeat step 1 with a different set of inputs. Otherwise, proceed to step 4.

3. Adjust the current weights according to 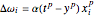, where 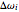is the change in the neuron's weight, is the learning rate, 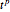is the target output given the input set 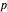, 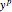is the real output of the neuron given the input set 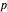after being passed through the threshold set by the bias , and is the input.

4. Repeat the algorithm from step 1 until for every vector pair.

Perceptron training rule: When the perceptron training rule algorithm is selected, the steps are:

1. Evaluate the network according to the equation: .

2. If the result of step 1 is greater than zero, ; if it is less than zero, .

3. If the current output 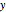is already equal to the desired output , repeat step 1 with a different set of inputs. If the current output 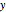is different from the desired output , proceed to step 4.

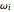
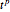
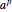
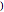
4. Adjust the current weights according to: 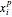, where 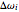is the change in the neuron's weight, is the learning rate, 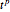is the target output given the input set 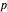, 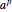is the real output of the neuron given the input set 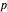without being passed through the threshold set by the bias , and is the input.

5. Repeat the algorithm from step 1 until for every vector pair.

It can be observed that the perceptron training rule gets to a finite value of weights and then stays in it, whereas the delta rule approaches certain asymptotic values but never reaches them. This is because of the origin of both rules. The perceptron training rule has a geometric value that can work directly with the value of the evaluated neuron after the threshold (logic values of 0 and 1), while the delta rule has its origin in the gradient error descent, so it works with the net value of the output without being passed through the threshold.

Reference

[1] K. Gurney, An Introduction to Neural Networks, Boca Raton, FL: CRC Press, 1997.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send